22 January 2018
Let’s start by loading some data from the Union Army Data Project. This project gathered extensive data on Union Army recruits from a wide variety of sources. In this tutorial, we will work with the data on the recruits’ heights, race, and wealth.
I have created the following data files for use with this tutorial:
Let’s try loading each dataset individually and then take a look at the data using the describe and summarize commands. How we load the data will depend on what format the data are in. The simplest scenario is a dataset already in Stata (.dta) format. In this case we simply open the data using the use command:
. clear . cd /Users/jparman/Dropbox/courses/400-spring-18/stata-modules/ /Users/jparman/Dropbox/courses/400-spring-18/stata-modules . use UA-heights.dta
The first command, clear, tells Stata to clear out any data that may currently be open. If you do not issue the clear command and there is already data in memory that has changed since last being saved, Stata will give you an error message. The second command, cd, changes the current directory to the one containing our data file. Note that you should change this to point to the directory where you saved the data files. Finally, the use command opens our dataset. Now we can take a quick look at the data with a few basic commands:
. describe
Contains data from UA-heights.dta
obs: 39,211
vars: 3 8 Apr 2018 09:18
size: 666,587
──────────────────────────────────────────────────────────────────────────────────────────────────────────────
storage display value
variable name type format label variable label
──────────────────────────────────────────────────────────────────────────────────────────────────────────────
recid double %10.0g recid
rh_feet1 byte %10.0g rh_feet1
rh_inch1 double %10.0g rh_inch1
──────────────────────────────────────────────────────────────────────────────────────────────────────────────
Sorted by: recid
. sum
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
recid │ 39,211 2.16e+09 1.20e+09 1.01e+08 7.10e+09
rh_feet1 │ 39,211 5.064829 .2546785 1 7
rh_inch1 │ 38,851 6.873358 2.72 0 11.875
The describe command tells you about the dataset, giving you information on the number of variables, the number of observations, and the data storage types for each variable. In this case, all three variables contain numbers. Numbers can be stored in several formats including byte, int, long, float, or double depending on how large the numbers get and how many digits they contain after the decimal place. The other variable type you will typically encounter is a string. The second command, sum, is an abbreviation for the summarize command and provides basic descriptive statistics of the data. Note that in this case we are told the number of observations for each variable as well as the mean, standard deviation, minimum and maximum. If we would like a little more information, we can include the detailed option:
. sum, detail
recid
─────────────────────────────────────────────────────────────
Percentiles Smallest
1% 1.01e+08 1.01e+08
5% 4.01e+08 1.01e+08
10% 1.20e+09 1.01e+08 Obs 39,211
25% 1.31e+09 1.01e+08 Sum of Wgt. 39,211
50% 2.20e+09 Mean 2.16e+09
Largest Std. Dev. 1.20e+09
75% 2.42e+09 7.10e+09
90% 3.20e+09 7.10e+09 Variance 1.43e+18
95% 5.10e+09 7.10e+09 Skewness 1.685253
99% 7.10e+09 7.10e+09 Kurtosis 7.428308
rh_feet1
─────────────────────────────────────────────────────────────
Percentiles Smallest
1% 5 1
5% 5 1
10% 5 2 Obs 39,211
25% 5 2 Sum of Wgt. 39,211
50% 5 Mean 5.064829
Largest Std. Dev. .2546785
75% 5 6
90% 5 6 Variance .0648611
95% 6 6 Skewness 2.838849
99% 6 7 Kurtosis 17.57112
rh_inch1
─────────────────────────────────────────────────────────────
Percentiles Smallest
1% 0 0
5% 1 0
10% 3 0 Obs 38,851
25% 5.25 0 Sum of Wgt. 38,851
50% 7 Mean 6.873358
Largest Std. Dev. 2.72
75% 9 11.75
90% 10 11.75 Variance 7.398401
95% 11 11.825 Skewness -.6298667
99% 11.5 11.875 Kurtosis 3.006998
Notice that to include an option for the command, we simply add a comma and then the appropriate option after the comma. If you are curious about what options you can add to a command, you can check the Stata help files for that command. An easy way to do this is to simply type help commandname into the command line where commandname is the command you would like options for. These help files are also very useful for learning the proper syntax for using a command.
These summary statistics are useful, but it also useful to take a look at a few individual observations to get a feel for the data. One option would be to open the data browser but, if you are like me and prefer to do everything from the command line, you can display several observations using the list command:
. list in 1/5
┌─────────────────────────────────┐
│ recid rh_feet1 rh_inch1 │
├─────────────────────────────────┤
1. │ 1.005e+08 5 8.5 │
2. │ 1.005e+08 5 8 │
3. │ 1.005e+08 5 10 │
4. │ 1.005e+08 5 10 │
5. │ 1.005e+08 5 5 │
└─────────────────────────────────┘
The list command by itself would list all of the observations. Given that there are 38851 observations, we do not want to do this. Including the in 1/5 option tells Stata to list observations one through five. We may also want to look at only the smallest or largest values when we list the data. One way we could do this is to sort our data. Let’s say we want to look at the five shortest recruits. We can do this by first sorting the recruits from shortest to tallest using the sort command:
. sort rh_feet1 rh_inch1
. list in 1/5
┌─────────────────────────────────┐
│ recid rh_feet1 rh_inch1 │
├─────────────────────────────────┤
1. │ 2.009e+08 1 5 │
2. │ 4.006e+08 1 6.5 │
3. │ 4.009e+08 2 10.5 │
4. │ 4.009e+08 2 . │
5. │ 2.009e+08 2 . │
└─────────────────────────────────┘
Stata will sort from smallest to largest on the first variable (rh_feet1) and then by the second variable (rh_inch1) within observations sharing the same value for the first variable. Here our shortest recruits appear to be under two feet tall, we’ll chalk that up to transcription errors.
Alternatively, we could sort the data from largest to smallest. To do this, we need to use a more flexible version of the sort command, gsort, that allows you to do both ascending and descending sorts. To do a descending sort, you simply add a minus sign in front of the variable name:
. gsort -rh_feet1 -rh_inch1
. list in 1/5
┌─────────────────────────────────┐
│ recid rh_feet1 rh_inch1 │
├─────────────────────────────────┤
1. │ 1.310e+09 7 .5 │
2. │ 2.107e+09 6 11.5 │
3. │ 1.309e+09 6 11 │
4. │ 3.101e+09 6 11 │
5. │ 1.408e+09 6 11 │
└─────────────────────────────────┘
Now let’s try loading the same data, but starting with the other file formats. First we’ll try the CSV file:
. clear
. insheet using UA-heights.csv, comma names
(3 vars, 39,211 obs)
. sum
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
recid │ 39,211 2.16e+09 1.20e+09 1.01e+08 7.10e+09
rh_feet1 │ 39,211 5.064829 .2546785 1 7
rh_inch1 │ 38,851 6.873358 2.72 0 11.875
The command insheet is used to read in data that is not in Stata format but is instead either comma or tab separated data with one observation per row. Here we have used the options comma and names. The comma option specifies that the file has comma-separated values (rather than tab-separated). The names option tells Stata that the first row of the file contains variable names rather than data.
The command for loading in an Excel file is slightly different. For an Excel file, we need to use the import command, specifying that we are importing an Excel file:
. clear
. import excel using UA-heights.xlsx, firstrow
. sum
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
recid │ 39,211 2.16e+09 1.20e+09 1.01e+08 7.10e+09
rh_feet1 │ 39,211 5.064829 .2546785 1 7
rh_inch1 │ 38,851 6.873358 2.72 0 11.875
We included the firstrow option to tell Stata that the first row of the Excel file contains variable names. There are many other options you can include to import only certain variables or ranges of the data. Note that if you ever want to save data in a non-Stata format (e.g., a CSV or Excel file), the insheet and import commands have their counterparts outsheet and export.
Log files and do files are an invaluable way to keep track of your work in Stata, ensure that you can reproduce your results, and save yourself a tremendous amount of time by not having to reissue the same commands over and over again. A log file is simply a file that contains all of the output shown on the Stata results screen. You can start and stop a log file using the log command:
. log using myfirstlogfile, replace name(myfirstlogfile)
──────────────────────────────────────────────────────────────────────────────────────────────────────────────
name: myfirstlogfile
log: /Users/jparman/Dropbox/courses/400-spring-18/stata-modules/myfirstlogfile.smcl
log type: smcl
opened on: 9 Apr 2018, 14:18:39
. sum
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
recid │ 39,211 2.16e+09 1.20e+09 1.01e+08 7.10e+09
rh_feet1 │ 39,211 5.064829 .2546785 1 7
rh_inch1 │ 38,851 6.873358 2.72 0 11.875
. log close myfirstlogfile
name: myfirstlogfile
log: /Users/jparman/Dropbox/courses/400-spring-18/stata-modules/myfirstlogfile.smcl
log type: smcl
closed on: 9 Apr 2018, 14:18:39
──────────────────────────────────────────────────────────────────────────────────────────────────────────────
For the log file command, I specified a file name (first-log-file) and added the replace option. This option tells Stata to overwrite the file if it already exists. If we had instead included the append command, Stata would keep whatever is in the existing log file and add to it. The name(myfirstlogfile) option let’s you specify a name to refer to the log file. Typically you can exclude this option.
By default, Stata saves log files in the SMCL format, Stata’s own output language. If you were to open the log file in a text editor or word processing program, it would look like gibberish. If you would prefer a format that is easily viewed in a text editor or word processing program, you can save the log file as a standard text file by including the text option after the comma. The resulting log file will have a .log extension.
Everything you do in Stata will be recorded to the log file until you issue the log close command. Now let’s take a look at our log file. First, let’s double check that it was created just to practice looking for files. To look for it, we will use the ls command:
. ls *.smcl -rw-r--r--@ 1 jparman staff 741 Jan 23 09:40 first-log-file.smcl -rw-r--r--@ 1 jparman staff 913 Jan 23 10:04 firstlogfile.smcl -rw-r--r-- 1 jparman staff 905 Apr 9 14:18 myfirstlogfile.smcl -rw-r--r--@ 1 jparman staff 7651 Apr 9 14:18 stata-modules-400-s18.smcl . view myfirstlogfile.smcl
This command lists the contents of the current directory. If I had only typed ls, every file and folder in the current directory would be listed. However, I only wanted to check for the log file which I knew should have a .smcl extension. Including *.smcl will only list files ending in .smcl. The asterisk allows for anything before .smcl. This approach to listing files in the directory can be very useful when you are trying to find the exact name of a data file you are trying to load or when you are checking that you are in the correct directory. We can see that Stata did indeed save our log file as firstlogfile.smcl. If you wanted to look at the log file within Stata, you could do so with the view command
. view myfirstlogfile.smcl
Do files contain a series of Stata commands that you execute by running the file with the do command. In general, you should use a do file to do all of your data cleaning and analysis. It means you do not have to type in a long series of commands each time you want to rerun your analysis, allows another person to easily replicate your analysis, and lets anyone see exactly how the data was manipulated and analyzed.
To create a do file, you can use Stata’s do file editor, which can be accessed by entering doedit in the command line, or you can use any text editor of your choice, saving your file with a .do extension. Among the files for this tutorial is an example do file named myfirstdofile.do. To take a look at the do file, open it in a text editor or by typing doedit myfirstdofile.do in the command line.
Notice that the the first few lines of the do file all begin with an asterisk. This tells Stata to ignore these lines when executing the do file. In general, it is helpful to document the do file using these sorts of lines. At the top of the file, include lines explaining what the do file is and then include documentation statements throughout the file explaining what each section of the do file is doing or providing any important notes about the data being used. This is a relatively simple do file with an excessive amount of documentation. However, when your do files start getting very long and accomplish very complicated things, good documentation becomes very important.
Let’s see what happens when we run the do file:
. do myfirstdofile.do
. * This is a basic do file to accompany the Stata Tutorial available
. * at http://jmparman.people.wm.edu/stata-tutorials/historical-income-and-wealth-distributions.html
. *
. * This file was created using a text editor and saved with the .do extension.
. *
. * To run the file from the command line, simply enter the following command: do myfirstdofile.do
. *
.
.
. * Create a log file to keep track of the output when running the do file
.
. log using myfirstlogfile, replace name(myfirstlogfile)
──────────────────────────────────────────────────────────────────────────────────────────────────────────────
name: myfirstlogfile
log: /Users/jparman/Dropbox/courses/400-spring-18/stata-modules/myfirstlogfile.smcl
log type: smcl
opened on: 9 Apr 2018, 14:18:40
.
. * Start by clearing out any open data
.
. clear
.
. * Load the Union Army height data
.
. cd /Users/jparman/Dropbox/courses/400-spring-18/stata-modules/
/Users/jparman/Dropbox/courses/400-spring-18/stata-modules
. use UA-heights.dta
.
. * Create a new variable that gives the recruits' overall heights in inches
.
. gen height_in_inches = rh_feet1*12 + rh_inch1
(360 missing values generated)
.
. * Save the data to a new file, close the dataset and then close the log file
.
. save UA-heights-in-inches.dta, replace
file UA-heights-in-inches.dta saved
. clear
. log close myfirstlogfile
name: myfirstlogfile
log: /Users/jparman/Dropbox/courses/400-spring-18/stata-modules/myfirstlogfile.smcl
log type: smcl
closed on: 9 Apr 2018, 14:18:40
──────────────────────────────────────────────────────────────────────────────────────────────────────────────
.
end of do-file
Running the do file is exactly like entering each command from the do file into the command line.
The importance of using do files cannot be overstated. Even if you figure out how you want to manipulate and analyze your data by entering different commands in the command line one by one or by using the graphical menus in Stata, you should always create a do file that runs the full set of commands you ultimately decide to use. This will let you easily replicate your analysis, make tweaks to your analysis later on, and let you know where your datasets came from and how your variables were generated. At the end of a project, you should have do files that do everything necessary to go from the original raw data to your final results.
One of the most common things you will need to do is generate new variables in Stata. In this section, we will go over some of the basics of creating a new variable and changing the values of an existing variable. Let’s start by opening up the Union Army height data and taking a look at it:
. clear
. use UA-heights.dta
. sum
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
recid │ 39,211 2.16e+09 1.20e+09 1.01e+08 7.10e+09
rh_feet1 │ 39,211 5.064829 .2546785 1 7
rh_inch1 │ 38,851 6.873358 2.72 0 11.875
Notice that we have two different height variables, rh_feet1 and rh_inch1. From the summary statistics, it is fairly clear that rh_feet1 is indeed measured in feet while rh_inch1 is measured in inches. We would probably prefer to have a single variable for height combining these two values. Let’s create a new variable called total_height that combines the variables:
. gen total_height = rh_feet1 * 12 + rh_inch1 (360 missing values generated)
To create the variable, we use the generate command which can be abbreviated as gen. After gen, we specified the name of the new variable to be created and then gave an expression for what the variable should equal. In this case, total height is equal to the value for the feet component of height multiplied by 12 (to convert to inches) plus the value for the inches component of height. An asterisk denoted multiplication and a plus sign denoted addition. In general, the basic arithmetic operators in Stata are:
There are a wide range of other mathematical functions you can use. See Stata’s manual page for functions and expressions.
Notice that the generate command gave us a message about missing values. To see what’s going on, we can summarize the observations that ended up with a missing value for height:
. sum rh_feet1 rh_inch1 if total_height==.
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
rh_feet1 │ 360 5.775 .4916433 2 6
rh_inch1 │ 0
In the above command, we used an if statement to restrict the observations summarized to just those with a missing value for total_height (the value for a missing numerical variable is a period, the value for a missing string variable is ""). Notice that when we generated our height variable, we used a single equals sign. When we used the if statement, we used a double equal sign. This is because in the generate command, we were using a arithmetic operator while in the if statement, we are using a relational operator. The basic Stata relational operators are:
For nearly any command, you can restrict the observations used by the command with an if statement that uses a combination of these operators. With that aside out of the way, let’s now look at the missing observations. As we can see from the output of the summarize command, these observations do have values for rh_feet1 but do not have values for rh_inch1: these are presumably recruits who were exactly five or six feet tall. For these recruits, we would like to replace their missing total height with their rh_feet1 value (multiplied by twelve). We can do this with the replace command:
. replace total_height = rh_feet1 * 12 if total_height==. & rh_feet1~=. (360 real changes made)
Notice that the if statement restricts the changes to observations missing a total_height value but not missing a rh_feet1 value. The ampersand is a logical operator denoting the `and’ operator. The basic Stata logical operators are:
Note that these can be combined into longer logical statements using parentheses:
Now let’s think about working with categorical variables. To do this, we will switch datasets to the one containing the races of the Union Army recruits, UA-race.dta. Before we open it up, let’s first save our modified height dataset:
. save UA-heights-revised.dta, replace file UA-heights-revised.dta saved
I have saved the height data with a new file name. We could have overwritten the original height data but I strongly recommend against doing this. In general, it is good practice never to overwrite your original data file. This way, if you ever make a mistake, say dropping a variable that you didn’t mean to drop or a set of observations you didn’t think you would need but turn out to be useful, you can always reconstruct your dataset from the original file (using that do file you were very smart to maintain). Now that we have our revised height dataset saved, let’s open up the race dataset:
. clear
. use UA-race.dta
. list in 1/5
┌──────────────────────────────────────────────────────────────────┐
│ recid reccol_0 reccol_1 reccol_5 reccol_6 reccol_7 │
├──────────────────────────────────────────────────────────────────┤
1. │ 1.005e+08 W │
2. │ 1.005e+08 W W W W │
3. │ 1.005e+08 W │
4. │ 1.005e+08 W W W W │
5. │ 1.005e+08 W W │
└──────────────────────────────────────────────────────────────────┘
Notice that we have several variables, all coding race (each one corresponds to a different year of observation for the recruit). The race variable is coded as a single letter: `W’ for white, `B’ for black, `M’ for mulatto, and `I’ for Indian. To see the distribution of these codes (or to confirm how many codes there are), we can use Stata’s tabulate command:
. tab reccol_0
reccol_0 │ Freq. Percent Cum.
────────────┼───────────────────────────────────
B │ 1,251 8.11 8.11
I │ 5 0.03 8.14
M │ 18 0.12 8.26
W │ 14,151 91.74 100.00
────────────┼───────────────────────────────────
Total │ 15,425 100.00
Rather than keeping track of several different race variables, let’s combine them into a single observation. We will begin by generating a new race variable equal to the value of reccol_:
. gen race = reccol_0 (11,140 missing values generated)
Many recruits have a missing value for reccol_0 but have race reported in a different year. Let’s work our way through these additional years, replacing race if it is missing from the first year when a value appears in a later year:
. tab race
race │ Freq. Percent Cum.
────────────┼───────────────────────────────────
B │ 1,251 8.11 8.11
I │ 5 0.03 8.14
M │ 18 0.12 8.26
W │ 14,151 91.74 100.00
────────────┼───────────────────────────────────
Total │ 15,425 100.00
. replace race = reccol_1 if race==""
(744 real changes made)
. replace race = reccol_5 if race==""
(5,307 real changes made)
. replace race = reccol_6 if race==""
(3,486 real changes made)
. replace race = reccol_7 if race==""
(1,603 real changes made)
. tab race
race │ Freq. Percent Cum.
────────────┼───────────────────────────────────
B │ 2,197 8.27 8.27
I │ 7 0.03 8.30
M │ 175 0.66 8.96
W │ 24,186 91.04 100.00
────────────┼───────────────────────────────────
Total │ 26,565 100.00
When just using reccol_0, we only had about 15,000 recruits with race observed. By using the additional years we have increased that number to over 26,000.
For doing analysis, what we really want are indicator variables taking a value of zero or one to indicate a particular race. There are a couple of ways we can accomplish this. We will start with a very simple approach, creating an indicator variable for a recruit being white:
. gen white = . (26,565 missing values generated) . replace white = 1 if race == "W" (24,186 real changes made) . replace white = 0 if race == "B" | race == "M" | race == "I" (2,379 real changes made)
This may not seem particularly helpful at the moment, but it will become quite useful when running regressions later on. Before moving on, let’s save our dataset so that we will not need to redo all of the steps we took to create the white indicator variable. We will also drop the reccol variables since we no longer need them.
. drop reccol* . save UA-race-revised.dta, replace file UA-race-revised.dta saved
Notice the use of the asterisk in the drop command. This is a wildcard; it tells Stata to include all variables that start with the letters reccol. If we had placed the asterisk at the beginning of reccol, Stata would drop all variables ending with reccol.
So far all of the variables we have generated have been numerical variables. The expressions we used are all fairly straightforward arithmetic where you could likely have guessed how to write out an expression to achieve the calculation you wanted. String variables are going to be a different story as the commands to manipulate them are a little less intuitive. Let’s open up the data for recruits’ birth places and birth dates to learn a bit about working with string variables.
. clear
. use UA-birth-states-and-dates.dta
. describe
Contains data from UA-birth-states-and-dates.dta
obs: 44,817
vars: 3 21 Jan 2018 10:02
size: 806,706
──────────────────────────────────────────────────────────────────────────────────────────────────────────────
storage display value
variable name type format label variable label
──────────────────────────────────────────────────────────────────────────────────────────────────────────────
recid double %10.0g recid
rb_date1 str8 %9s rb_date1
rb_stat1 str2 %9s rb_stat1
──────────────────────────────────────────────────────────────────────────────────────────────────────────────
Sorted by:
. list in 1/5
┌─────────────────────────────────┐
│ recid rb_date1 rb_stat1 │
├─────────────────────────────────┤
1. │ 1.005e+08 EN │
2. │ 1.005e+08 18410315 NY │
3. │ 1.005e+08 CT │
4. │ 1.005e+08 18450610 CT │
5. │ 1.005e+08 18431104 CT │
└─────────────────────────────────┘
Notice that in addition to our standard recruit ID variable, we have one variable for the recruits birth date and one for his birth state. If we look at the output from the describe command, we can see that both are string variables. When listing the data, it is clear that birth date is in the format YYYYMMDD and birth state is the two-letter abbreviation for the state (or country).
Let’s start by creating a new string variable that is simply the year of birth. What we need to do is take the first four characters of the birth date string. The substr command will do the trick:
. gen birthyear = substr(rb_date1,1,4) (25,239 missing values generated)
The substr function required three arguments, first the string variable we are taking a substring of (rb_date1), second the position in the string where we want the substring to start (the first character in this case) and finally the number of characters we want in the substring. We can follow a similar approach to create variables for month and day of birth:
. gen birthmonth = substr(rb_date1,5,2)
(25,239 missing values generated)
. gen birthday = substr(rb_date1,7,2)
(25,239 missing values generated)
. list rb_date1 birthyear birthmonth birthday in 1/5
┌───────────────────────────────────────────┐
│ rb_date1 birthy~r birthm~h birthday │
├───────────────────────────────────────────┤
1. │ │
2. │ 18410315 1841 03 15 │
3. │ │
4. │ 18450610 1845 06 10 │
5. │ 18431104 1843 11 04 │
└───────────────────────────────────────────┘
Suppose that we wanted nicely formatted dates of the form `Month Day, Year’. We can do this by concatenating the strings:
. gen birthdate_formatted = birthmonth + " " + birthday + ", " + birthyear if birthmonth~="" & birthday~="" &
> birthyear~=""
(25,239 missing values generated)
. list birthdate_formatted in 1/5
┌─────────────┐
│ birthdate~d │
├─────────────┤
1. │ │
2. │ 03 15, 1841 │
3. │ │
4. │ 06 10, 1845 │
5. │ 11 04, 1843 │
└─────────────┘
Notice that we are simply adding the strings together, inserting our additional spaces and commas. I have added an if statement to make certain that the recruit actually has values for the different birth date components. The double quotes with nothing between them indicates a missing value for a string variable (a missing value for a numerical variable is given as a period in Stata). So each component of the if statement is requiring that the relevant piece of the birth date be non-missing. Our birth dates look fairly nice now, but there are a couple of issues. First, I don’t like the look of having the zeros in front of single digit numbers. Let’s get rid of those with by using the subinstr function:
. replace birthdate_formatted = subinstr(birthdate_formatted," 0"," ",1) (4,179 real changes made) . replace birthdate_formatted = subinstr(birthdate_formatted,"0","",1) if strpos(birthdate_formatted,"0")==1 (10,379 real changes made)
The first replace command finds and replaces all of the leading zeros for the birth day (these leading zeros will all have a space in front of them). The subinstr function took four arguments. First was the variable we wanted to substitute into (birthdate_formatted), second was the substring we wanted to replace (zero with a leading space), third was the substring we wanted to replace it with (simply a space) and finally the number of instances of the substring we wanted to replace (just the first one in this case).
The second replace command finds and replaces all of the leading zeros for the birth month (these leading zeros will not have a space in front of them). We are replacing them with an empty string, denoted by double quotes with nothing between them. This is the equivalent of simply removing the substring. Notice that I included an if statement using the strpos function. This function searches the string variable you specify (birthdate_formatted) for the substring you specify (“0”) and returns its starting position in the string for the first instance (or zero if it cannot be found). I am using it here so that we only replace the first zero when it is the first character in the string, we do not want to replace any of the other zeros.
The final thing we need to do for nicely formatted dates is to convert the months from numbers to the month name fully spelled out. We can do this once again with the help of the subinstr and strpos commands. In general, we can use subinstr to replace the month number with the month name. We will need a couple of if statements to make certain that we don’t mix up January and November (both end in 1) and February and December (both end in 2):
. replace birthdate_formatted = subinstr(birthdate_formatted,"1 ","January ",1) if strpos(birthdate_formatted,
> "1 ")==1
variable birthdate_formatted was str11 now str16
(1,224 real changes made)
. replace birthdate_formatted = subinstr(birthdate_formatted,"2 ","February ",1) if strpos(birthdate_formatted
> ,"2 ")==1
variable birthdate_formatted was str16 now str17
(1,188 real changes made)
. replace birthdate_formatted = subinstr(birthdate_formatted,"3 ","March ",1)
(1,401 real changes made)
. replace birthdate_formatted = subinstr(birthdate_formatted,"4 ","April ",1)
(1,164 real changes made)
. replace birthdate_formatted = subinstr(birthdate_formatted,"5 ","May ",1)
(1,131 real changes made)
. replace birthdate_formatted = subinstr(birthdate_formatted,"6 ","June ",1)
(1,026 real changes made)
. replace birthdate_formatted = subinstr(birthdate_formatted,"7 ","July ",1)
(1,016 real changes made)
. replace birthdate_formatted = subinstr(birthdate_formatted,"8 ","August ",1)
(1,168 real changes made)
. replace birthdate_formatted = subinstr(birthdate_formatted,"9 ","September ",1)
variable birthdate_formatted was str17 now str18
(1,061 real changes made)
. replace birthdate_formatted = subinstr(birthdate_formatted,"10 ","October ",1)
(1,139 real changes made)
. replace birthdate_formatted = subinstr(birthdate_formatted,"11 ","November ",1)
(1,094 real changes made)
. replace birthdate_formatted = subinstr(birthdate_formatted,"12 ","December ",1)
(1,189 real changes made)
. list birthdate_formatted in 1/5
┌──────────────────┐
│ birthdate_form~d │
├──────────────────┤
1. │ │
2. │ March 15, 1841 │
3. │ │
4. │ June 10, 1845 │
5. │ November 4, 1843 │
└──────────────────┘
The dates look pretty good now. Suppose that this was the initial format for the birth dates and you wanted to extract the birth years. You could use our original approach of pulling out the appropriate four-character substring. However, it is a bit trickier in this case because the starting position of the year in the string varies due to the length of the month and day components. Let’s quickly look at three different ways to pull out the birth year to highlight a few other string functions.
. gen year_approach_1 = reverse(substr(reverse(birthdate_formatted),1,4))
(25,239 missing values generated)
. gen year_approach_2 = substr(birthdate_formatted,strpos(birthdate_formatted,",")+2,4)
(25,239 missing values generated)
. split birthdate_formatted, gen(birthdate_component) parse(",")
variables created as string:
birthdate_~1 birthdate_~2
. gen year_approach_3 = trim(birthdate_component2)
(25,239 missing values generated)
. list year_approach* in 1/5
┌────────────────────────────────┐
│ year_a~1 year_a~2 year_a~3 │
├────────────────────────────────┤
1. │ │
2. │ 1841 1841 1841 │
3. │ │
4. │ 1845 1845 1845 │
5. │ 1843 1843 1843 │
└────────────────────────────────┘
Details on all of the functions used above are available in the Stata manual pages for string functions. The first approach takes advantage of the reverse function. By reversing the birth date, the year will be at the start, letting us once again pull the first four characters as the year. After getting those characters, we then need to use the reverse command again to get the year digits back in the right order. The second approach uses the strpos command within the substr to find where the position of year is in the string (the position is two spaces after the comma). The third approach uses the split command. This command splits a string variable at each instance of the parse string (a comma in this case) and generates new string variables to contain each substring. In this case we want the substring coming after the comma, which is the second component (birthdate_component1 would contain the month and day). The trim command simply removes any leading or trailing spaces from the string.
Now suppose that we wanted to use birth year in our analysis. Perhaps we simply want to look at only recruits born after 1845. We have a slight problem. We know that birth year is a number, Stata still thinks it is a string. This means that Stata will not be able to interpret something like birthyear>1845. We need to convert birth year to a number. This is easily done with the destring command.
. destring birthyear, force replace
birthyear: contains nonnumeric characters; replaced as int
(25244 missing values generated)
. sum birthyear if birthyear>1845
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
birthyear │ 2,226 1846.858 1.059816 1846 1855
We included two options for the destring command. The replace option tells Stata to replace the current string variable with the new numerical variable rather than generating a new variable. The force option tells Stata to convert anything that doesn’t look like a number to missing value. Be very cautious when you use the force option. If you inadvertently had a stray character in your birth years, they would all get converted to missing values. Let’s clean up our dataset, save it and move on:
. destring birthmonth, force replace birthmonth: contains nonnumeric characters; replaced as byte (31016 missing values generated) . destring birthday, force replace birthday: contains nonnumeric characters; replaced as byte (31284 missing values generated) . keep recid birthyear birthmonth birthday birthdate_formatted rb_stat1 . save UA-birth-dates-and-states-revised.dta, replace file UA-birth-dates-and-states-revised.dta saved
Often times you will have multiple datasets that share a common variable, say individual or country, but otherwise contain different information that you would like to combine into a single dataset. This is where Stata’s merge command comes in. With the merge command, you can combine two datasets on that share a common variable identifying observations. In the case of our Union Army data, this is the recid variable giving the recruit ID number.
Let’s merge the height data with the data on recruit race:
. clear
. use UA-heights-revised.dta
. sort recid
. save UA-heights-revised.dta, replace
file UA-heights-revised.dta saved
. clear
. use UA-race-revised.dta
. sort recid
. merge 1:1 recid using UA-heights-revised.dta
Result # of obs.
─────────────────────────────────────────
not matched 19,862
from master 3,608 (_merge==1)
from using 16,254 (_merge==2)
matched 22,957 (_merge==3)
─────────────────────────────────────────
Notice that we sorted both datasets by our merging variable. Also notice that we declared this a 1:1 merge. This means that each observation in the master dataset should match one and only one observation in the using dataset. Suppose instead that we were merging the recruits on the basis of their birthstate to a dataset containing state-level variables. In this case, each observation in our using dataset (the state-level data) would match to many observations in the master dataset (the recruit-level data). In this case, we would be doing a many-to-one merge and would use the following syntax: merge m:1 stateid using state-level-data.dta.
Stata has reported how many of the observations could be successfully merged. We can see that the majority of observations were successfully merged, but there are over 3,000 observations in the master dataset (UA-race.dta) that could not be merged and over 16,000 observations in the using dataset (UA-heights.dta) that could not be merged. This same information is contained in the newly created _merge variable. Note that if you are doing multiple merges, you will need to rename the existing _merge variable to avoid getting an error when running the next merge command.
In this case, we shouldn’t be too concerned with how many of these observations could not be merged across the datasets. Many recruits in the height dataset are not in the race dataset and many of the recruits in the race dataset do not appear in the height dataset. However, if we were expecting the datasets to contain the same set of recruits, large numbers of unmatched observations would be a red flag suggesting something is wrong with the way we coded or selected the variable to merge on. If you are surprised by the number of unmatched observations, you can take a look at them by taking advantage of the _merge variable:
. sum if _merge==1
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
recid │ 3,608 6.93e+09 3.25e+09 1.11e+08 9.01e+09
race │ 0
white │ 3,608 .3492239 .4767909 0 1
rh_feet1 │ 0
rh_inch1 │ 0
─────────────┼─────────────────────────────────────────────────────────
total_height │ 0
_merge │ 3,608 1 0 1 1
. sum if _merge==2
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
recid │ 16,254 2.12e+09 1.27e+09 1.01e+08 7.10e+09
race │ 0
white │ 0
rh_feet1 │ 16,254 5.053218 .2330802 1 7
rh_inch1 │ 16,126 6.735483 2.665352 0 11.75
─────────────┼─────────────────────────────────────────────────────────
total_height │ 16,254 67.32105 2.740175 18.5 84.5
_merge │ 16,254 2 0 2 2
Let’s go ahead and merge in our wealth dataset, UA-wealth-long.dta. We’ll start by saving our merged height and race data and then opening up the wealth data to see how it is structured. Since we will be doing another merge, we’ll rename the _merge variable before saving the merged dataset.
. rename _merge height_merge . sort recid . save UA-heights-and-race.dta, replace file UA-heights-and-race.dta saved . clear . use UA-wealth-long.dta . sort recid . gen recid_part_1 = (recid - mod(recid,10000))/10000 . gen recid_part_2 = mod(recid,10000)
I have generated two new variables to make it easier to look at the recid variable given that recid is a nine digit number. This makes it too long to easily view. The two generate commands basically split the variable into its first five digits and its last four digits. The first command uses the mod function to subtract off the last four digits from the recid, leaving only the first five digits following by four zeros. Dividing by 10,000 then leaves only the first five digits. The second command simply uses the mod function to keep the last four digits. These new variables will help us see how the data is structured when we use the list command:
. list in 1/10
┌──────────────────────────────────────────────────────────┐
│ recid reclan recprp year recid_~1 recid_~2 │
├──────────────────────────────────────────────────────────┤
1. │ 1.005e+08 . . 1870 10050 1001 │
2. │ 1.005e+08 . 300 1860 10050 1001 │
3. │ 1.005e+08 . . 1870 10050 1008 │
4. │ 1.005e+08 1000 250 1860 10050 1008 │
5. │ 1.005e+08 . 400 1860 10050 1016 │
├──────────────────────────────────────────────────────────┤
6. │ 1.005e+08 . . 1870 10050 1016 │
7. │ 1.005e+08 . 75 1860 10050 1017 │
8. │ 1.005e+08 . . 1870 10050 1017 │
9. │ 1.005e+08 . 500 1860 10050 1075 │
10. │ 1.005e+08 . . 1870 10050 1075 │
└──────────────────────────────────────────────────────────┘
As we can see, we have multiple observations for each recruit in this dataset, one for 1860 and one for 1870. This means that each observation in our height and race dataset will match multiple observations in the wealth dataset, necessitating a many-to-one merge:
. sort recid
. merge m:1 recid using UA-heights-and-race.dta
Result # of obs.
─────────────────────────────────────────
not matched 36,674
from master 6 (_merge==1)
from using 36,668 (_merge==2)
matched 12,302 (_merge==3)
─────────────────────────────────────────
. rename _merge wealth_merge
. list in 1/2
┌───────────┬────────┬────────┬──────┬──────────┬──────────┬──────┬───────┬──────────┬──────────┐
1. │ recid │ reclan │ recprp │ year │ recid_~1 │ recid_~2 │ race │ white │ rh_feet1 │ rh_inch1 │
│ 1.005e+08 │ . │ . │ 1870 │ 10050 │ 1001 │ W │ 1 │ 5 │ 8.5 │
├───────────┴────────┴────────┼──────┴──────────┴──────────┴───┬--┴───────┴──────────┴──────────┤
│ total_~t │ height_me~e │ wealth_me~e │
│ 68.5 │ matched (3) │ matched (3) │
└─────────────────────────────┴────────────────────────────────┴────────────────────────────────┘
┌───────────┬────────┬────────┬──────┬──────────┬──────────┬──────┬───────┬──────────┬──────────┐
2. │ recid │ reclan │ recprp │ year │ recid_~1 │ recid_~2 │ race │ white │ rh_feet1 │ rh_inch1 │
│ 1.005e+08 │ . │ 300 │ 1860 │ 10050 │ 1001 │ W │ 1 │ 5 │ 8.5 │
├───────────┴────────┴────────┼──────┴──────────┴──────────┴───┬--┴───────┴──────────┴──────────┤
│ total_~t │ height_me~e │ wealth_me~e │
│ 68.5 │ matched (3) │ matched (3) │
└─────────────────────────────┴────────────────────────────────┴────────────────────────────────┘
As we can see, the first recruit in the dataset has an observation for his 1860 wealth values and an observation for his 1870 wealth values (which happen to be missing). The same height and race information has been merged to both of those observations. Finally, let’s follow the same procedure to merge in out birth state and birth date information:
. merge m:1 recid using UA-birth-dates-and-states-revised.dta
Result # of obs.
─────────────────────────────────────────
not matched 4,993
from master 1,591 (_merge==1)
from using 3,402 (_merge==2)
matched 47,385 (_merge==3)
─────────────────────────────────────────
. rename _merge bdate_merge
Our merged dataset currently has multiple observations per recruit, one for each year. This is a dataset in long format. You will often find it more useful to work with data in wide format, where there is one observation per individual with different variables to capture the values of characteristics in different time periods. Say, for example, that we wanted to see how recruits’ wealth in 1860 was correlated with their wealth in 1870. This is most easily accomplished if wealth in 1860 and wealth in 1870 are two separate variables allowing us to simply use Stata’s correlate command. Fortunately, we can use Stata’s reshape command:
. save UA-complete-data-long-format.dta, replace
file UA-complete-data-long-format.dta saved
. drop if year==.
(40,070 observations deleted)
. reshape wide reclan recprp, i(recid) j(year)
(note: j = 1860 1870)
Data long -> wide
─────────────────────────────────────────────────────────────────────────────
Number of obs. 12308 -> 6154
Number of variables 19 -> 20
j variable (2 values) year -> (dropped)
xij variables:
reclan -> reclan1860 reclan1870
recprp -> recprp1860 recprp1870
─────────────────────────────────────────────────────────────────────────────
. save UA-complete-data-wide-format.dta, replace
file UA-complete-data-wide-format.dta saved
. list in 1/2
┌───────────┬──────────┬──────────┬──────────┬──────────┬──────────┬──────────┬──────┬───────┬──────────┐
1. │ recid │ recla~60 │ recpr~60 │ recla~70 │ recpr~70 │ recid_~1 │ recid_~2 │ race │ white │ rh_feet1 │
│ 1.005e+08 │ . │ 300 │ . │ . │ 10050 │ 1001 │ W │ 1 │ 5 │
├───────────┼──────────┴┬─────────┴────┬─────┴────────┬-┴─────────┬┴──────────┼──────┴─────┬-┴──────────┤
│ rh_inch1 │ total_~t │ height_me~e │ wealth_me~e │ rb_stat1 │ birthy~r │ birthm~h │ birthday │
│ 8.5 │ 68.5 │ matched (3) │ matched (3) │ EN │ . │ . │ . │
├───────────┴───────────┴──────────────┴──────────┬───┴───────────┴───────────┴────────────┴────────────┤
│ birthd~d │ bdate_merge │
│ │ matched (3) │
└─────────────────────────────────────────────────┴─────────────────────────────────────────────────────┘
┌───────────┬──────────┬──────────┬──────────┬──────────┬──────────┬──────────┬──────┬───────┬──────────┐
2. │ recid │ recla~60 │ recpr~60 │ recla~70 │ recpr~70 │ recid_~1 │ recid_~2 │ race │ white │ rh_feet1 │
│ 1.005e+08 │ 1000 │ 250 │ . │ . │ 10050 │ 1008 │ W │ 1 │ 5 │
├───────────┼──────────┴┬─────────┴────┬─────┴────────┬-┴─────────┬┴──────────┼──────┴─────┬-┴──────────┤
│ rh_inch1 │ total_~t │ height_me~e │ wealth_me~e │ rb_stat1 │ birthy~r │ birthm~h │ birthday │
│ 8.5 │ 68.5 │ matched (3) │ matched (3) │ IR │ . │ . │ . │
├───────────┴───────────┴──────────────┴──────────┬───┴───────────┴───────────┴────────────┴────────────┤
│ birthd~d │ bdate_merge │
│ │ matched (3) │
└─────────────────────────────────────────────────┴─────────────────────────────────────────────────────┘
We needed to specify several things when using the reshape command. First, we included the word wide to indicate that we are reshaping the data into wide format. Then, we specified the variables that vary across years (reclan and recprp, our two wealth variables). Finally, in the options we specified the i variable (this is the variable that identifies individuals) and the j variable (the variable that identifies the time period).
When Stata converts the data to wide format, it needs to create new variables, one for each time period, for each of the time-varying variables. The variable names will be the original variable with the time period appended to it. In our case, Stata has created reclan1860, reclan1870, recprp1860 and recprp1870. All of the other variables, the ones that do not vary over time, retain their original variable names.
One nice feature is that once you have reshaped the data, Stata keeps track of your i and j variables. This allows you to easily convert the data back and forth between wide and long formats. For example, if you wanted to return to a long format, you would simply need to issue the command reshape long without needing to specify any additional information.
Let’s return to our original motivation for reshaping the data: looking at the correlation in wealth across years. With the data now in wide format, this is easily done:
. corr reclan* recprp*
(obs=236)
│ recla~60 recla~70 recpr~60 recpr~70
─────────────┼────────────────────────────────────
reclan1860 │ 1.0000
reclan1870 │ 0.6697 1.0000
recprp1860 │ 0.6218 0.4660 1.0000
recprp1870 │ 0.3762 0.4634 0.3704 1.0000
We can see that real estate wealth (reclan) is rather strongly correlated across years. Additionally, real estate and personal property wealth are highly correlated in 1860, with that correlation dropping off by 1870. The next sections will go into more detail about these variations in wealth to think about using graphs and regressions in Stata.
Stata has powerful graphing capabilities and offers you the chance to control many aspects of the graph. Unfortunately, this can also require setting many different options to get graphs the way you want them to look. It is often easiest to start building your graphs by clicking your way through the graphics menu and the subsequent options. Once you create a graph this way, Stata will construct the command line for your graph. You can then copy this command line and paste it into your do file so that you can easily reproduce the graph and make small changes to the options you have selected.
One of the most common types of graphs you will want to make is a scatter plot. Scatter plots are useful to display the basic relationship between two variables. Let’s use a scatter plot, using Stata’s twoway command, to look at the correlation we found between real estate wealth and personal property wealth:
. twoway (scatter recprp1860 reclan1860), ytitle("Personal property wealth, 1860") xtitle("Real estate wealth
> , 1860") graphregion(color(white)) bgcolor(white)
. graph export wealth-scatter-a.png, width(500) replace
(file wealth-scatter-a.png written in PNG format)

Here we have opted for a basic scatter plot by specifying scatter and then our vertical and horizontal axis variables. Other common types of twoway graphs include line and connected. We have added options to label the vertical and horizontal axes and to switch the graph’s background and border colors to white. There are an extensive number of other options that you can add, summarized here.
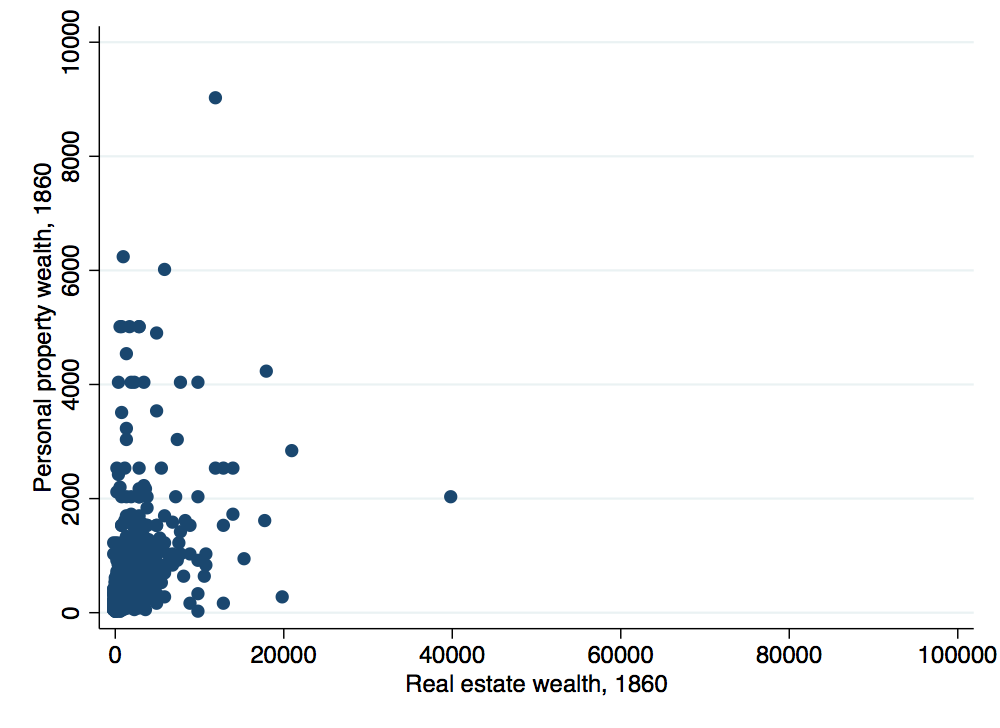
Notice that the graph does not look all that great. In particular, a few outliers are leading to the majority of observations being plotted in a very small region making it difficult to see what is going on. Let’s use an if statement to restrict the range of observations for a clearer graph:
. twoway (scatter recprp1860 reclan1860 if recprp1860<6000 & reclan1860<20000), ytitle("Personal property weal
> th, 1860") xtitle("Real estate wealth, 1860") graphregion(color(white)) bgcolor(white)
. graph export wealth-scatter-b.png, width(500) replace
(file wealth-scatter-b.png written in PNG format)
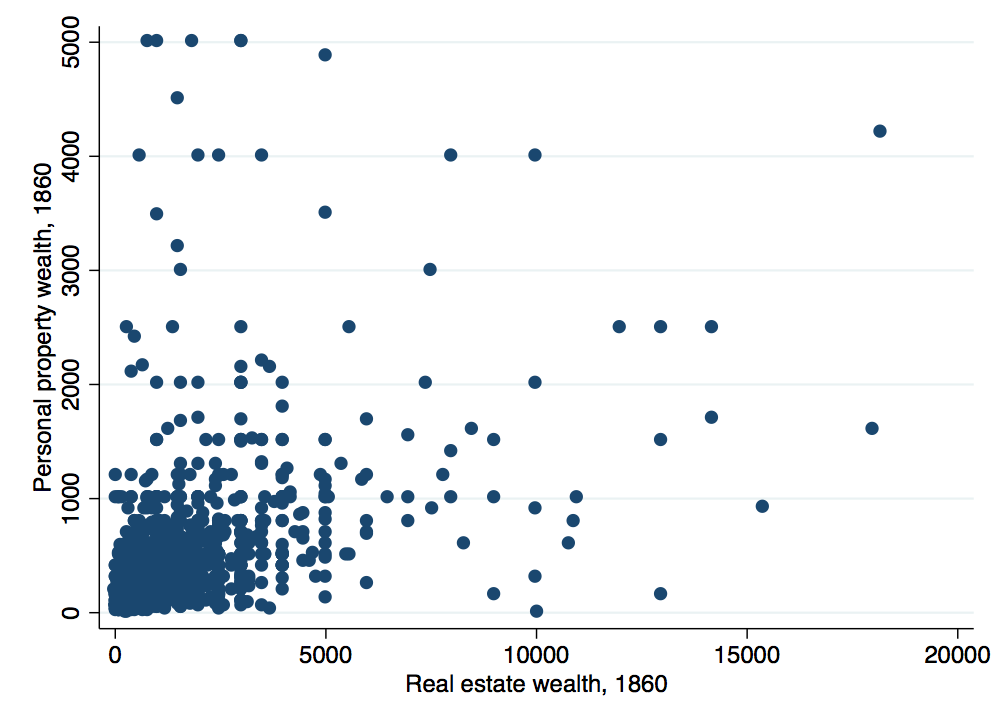
That certainly looks a bit better. However, when you have several hundred observations, it can often lead to a graph too cluttered to discern any real trends. One solution in this situation is to use the binscatter package (note that you need to install this package which can be done using the command ssc install binscatter). The binscatter package provides an easy way to produce binned scatterplots. It divides the data into evenly-spaced bins and then plots the mean x and y values within each bin. Let’s take a look:
. binscatter recprp1860 reclan1860 if recprp1860<6000 & reclan1860<20000, ytitle("Personal property wealth, 18
> 60") xtitle("Real estate wealth, 1860") graphregion(color(white)) bgcolor(white)
warning: nquantiles(20) was specified, but only 18 were generated. see help file under nquantiles() for explan
> ation.
. graph export wealth-scatter-c.png, width(500) replace
(file wealth-scatter-c.png written in PNG format)
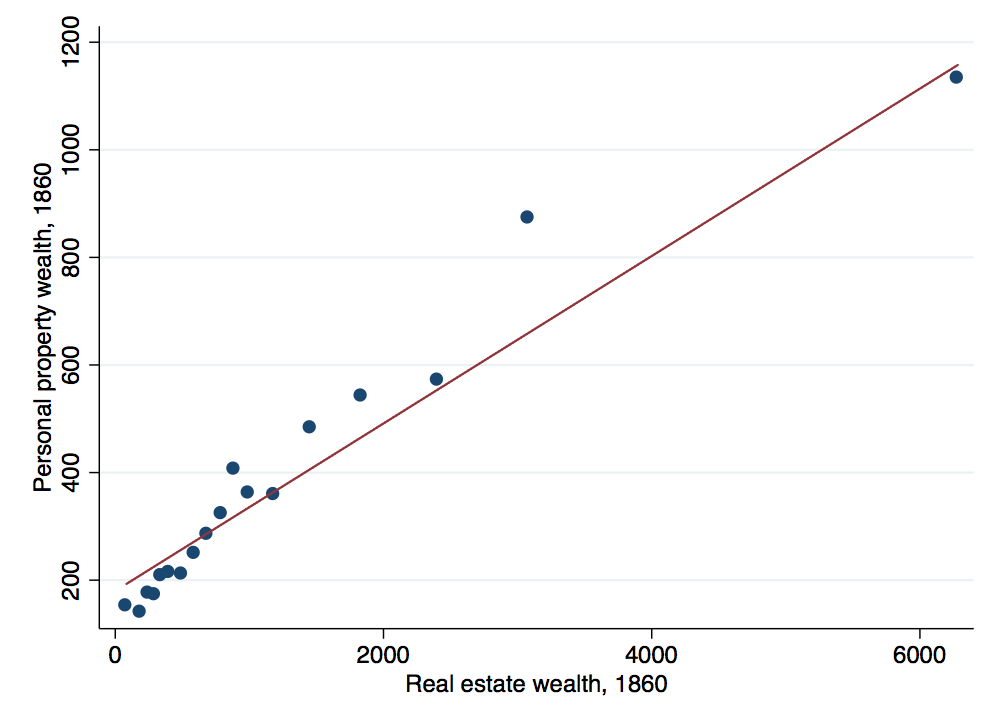
The binned scatterplot makes the positive relationship between the two types of wealth much clearer.
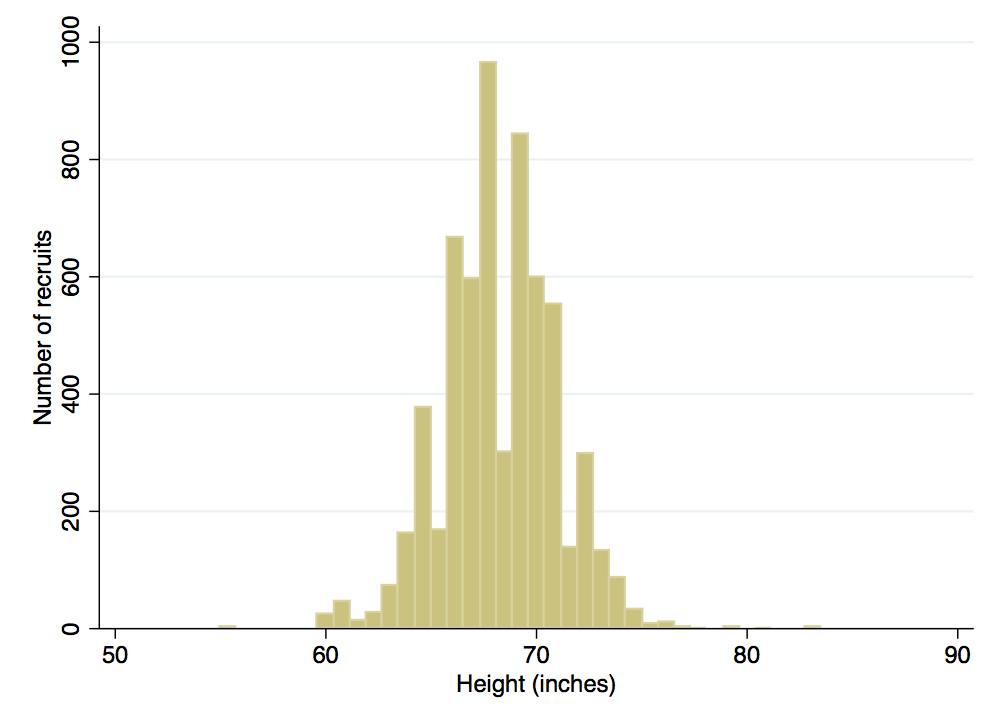
Now we’ll turn our attention to graphing the distribution of a single variable. In this case, a histogram is useful. Let’s use one to look at the distribution of recruit heights:
. histogram total_height if total_height>48, frequency ytitle(Number of recruits) xtitle(Height (inches)) grap > hregion(color(white)) bgcolor(white) (bin=37, start=55, width=.77027027) . graph export height-histogram.png, width(500) replace (file height-histogram.png written in PNG format)
Suppose that instead of looking at individual recruits, we instead wanted to look at differences across states. One thing we could do is collapse the data to the state level. Let’s give it a try:
. collapse (mean) birthyear_mean = birthyear height_mean=total_height recprp_mean = recprp1860 reclan_mean = r
> eclan1860 (median) birthyear_median = birthyear height_median = height recprp_median = recprp1860 reclan_med
> ian=reclan1860 (sum) white_recruits = white, by(rb_stat1)
. list in 1/5
┌──────────┬───────────┬──────────┬───────────┬───────────┬──────────┬──────────┬──────────┬──────────┐
1. │ rb_stat1 │ birth~ean │ heig~ean │ recpr~ean │ recla~ean │ birt~ian │ heig~ian │ recp~ian │ recl~ian │
│ │ 1830.2638 │ 68.47528 │ 285.9903 │ 745.86184 │ 1830 │ 3 │ 175 │ 570 │
├──────────┴───────────┴──────────┴───────────┴───────────┴──────────┴──────────┴──────────┴──────────┤
│ white_~s │
│ 231 │
└─────────────────────────────────────────────────────────────────────────────────────────────────────┘
┌──────────┬───────────┬──────────┬───────────┬───────────┬──────────┬──────────┬──────────┬──────────┐
2. │ rb_stat1 │ birth~ean │ heig~ean │ recpr~ean │ recla~ean │ birt~ian │ heig~ian │ recp~ian │ recl~ian │
│ AL │ 1832.3334 │ 70.2 │ 406.66666 │ 1162.5 │ 1842 │ 3 │ 200 │ 1162.5 │
├──────────┴───────────┴──────────┴───────────┴───────────┴──────────┴──────────┴──────────┴──────────┤
│ white_~s │
│ 5 │
└─────────────────────────────────────────────────────────────────────────────────────────────────────┘
┌──────────┬───────────┬──────────┬───────────┬───────────┬──────────┬──────────┬──────────┬──────────┐
3. │ rb_stat1 │ birth~ean │ heig~ean │ recpr~ean │ recla~ean │ birt~ian │ heig~ian │ recp~ian │ recl~ian │
│ AR │ 1843.5 │ 66.75 │ . │ . │ 1843.5 │ 3 │ . │ . │
├──────────┴───────────┴──────────┴───────────┴───────────┴──────────┴──────────┴──────────┴──────────┤
│ white_~s │
│ 2 │
└─────────────────────────────────────────────────────────────────────────────────────────────────────┘
┌──────────┬───────────┬──────────┬───────────┬───────────┬──────────┬──────────┬──────────┬──────────┐
4. │ rb_stat1 │ birth~ean │ heig~ean │ recpr~ean │ recla~ean │ birt~ian │ heig~ian │ recp~ian │ recl~ian │
│ BE │ 1836 │ 65.73913 │ 185.66667 │ 466.66667 │ 1838 │ 3 │ 177 │ 300 │
├──────────┴───────────┴──────────┴───────────┴───────────┴──────────┴──────────┴──────────┴──────────┤
│ white_~s │
│ 22 │
└─────────────────────────────────────────────────────────────────────────────────────────────────────┘
┌──────────┬───────────┬──────────┬───────────┬───────────┬──────────┬──────────┬──────────┬──────────┐
5. │ rb_stat1 │ birth~ean │ heig~ean │ recpr~ean │ recla~ean │ birt~ian │ heig~ian │ recp~ian │ recl~ian │
│ BN │ 1831.5 │ 66.85714 │ 183.33333 │ 950 │ 1832.5 │ 3 │ 200 │ 950 │
├──────────┴───────────┴──────────┴───────────┴───────────┴──────────┴──────────┴──────────┴──────────┤
│ white_~s │
│ 7 │
└─────────────────────────────────────────────────────────────────────────────────────────────────────┘
The collapse command is essentially averaging variable values across the observations in each group. We define the groups using the by() option. In this case, we used rb_stat1 as the by variable in order to aggregate the data up to the state level. Note that you can use multiple by variables. For example, had we used by(rb_stat1 white) we would get two observations per state, one aggregating all of the observations with white equal to zero and one aggregating all of the observations with white equal to one. We define which variables we want aggregated and how we want them aggregated in the main arguments of the command. First, I wanted the mean birth year, height, and 1860 wealth values for each state. To do this, I specified mean in parentheses and then followed this with each variable I wanted the mean of using the following syntax: newvariablename = originalvariablename. Next, I wanted the medians for the same variables. Finally, I wanted to know the total number of white recruits by state. I did this by specifying that I wanted the sum of the white variable (since it equals one for each white recruit, its sum should equal the total number of white recruits).
With our newly collapsed dataset, lets go ahead and take a look at the state-level relationship between height and real estate wealth.
. twoway (lfit reclan_mean height_mean if white_recruits>25) (scatter reclan_mean height_mean if white_recruit
> s>25, msymbol(none) mlabel(rb_stat1)), ytitle("Mean real estate wealth, 1860") xtitle("Mean recruit height (
> inches)") graphregion(color(white)) bgcolor(white) legend(off)
. graph export state-scatter-a.png, width(500) replace
(file state-scatter-a.png written in PNG format)
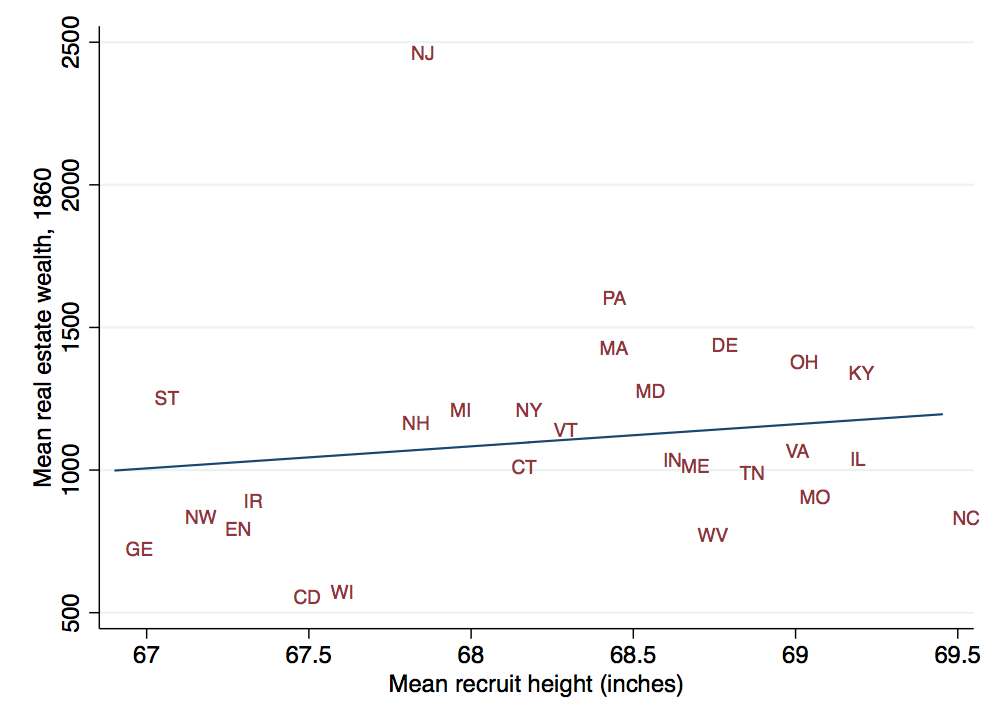
We’ve added a few new features relative to the previous graphs. First, we are combining two different graphs on the same plot. In the first set of parentheses, we are graphing a linear fit using lfit. In the second set of parentheses, we are using a scatterplot to show the data underlying that linear fit. The other new feature here is modifying the marker properties. Since our states are recorded using two-letter abbreviations, we can actually use these abbreviations as the marker on the graph. To do this, we first removed the standard marker symbols by specifying msymbol(none) and then we added marker labels based on the state names by specifying mlabel(rb_stat1). Now it is easy to see from the graph which data point corresponds to which state. Let’s do one more graph to delve even further into the seemingly endless features for formatting graphs:
. twoway (scatter recprp_mean height_mean if white_recruits>25, msymbol(default) mlabel(rb_stat1)) (lfit recpr
> p_mean height_mean if white_recruits>25) (qfit recprp_mean height_mean if white_recruits>25), ytitle("Mean p
> ersonal property wealth, 1860") xtitle("Mean height (inches)") legend(order(1 "Observed Values" - "Fitted Va
> lues:" 2 "Linear" 3 "Quadratic") cols(1) ring(0)) graphregion(color(white)) bgcolor(white)
(note: named style default not found in class symbol, default attributes used)
. graph export state-scatter-b.png, width(500) replace
(file state-scatter-b.png written in PNG format)
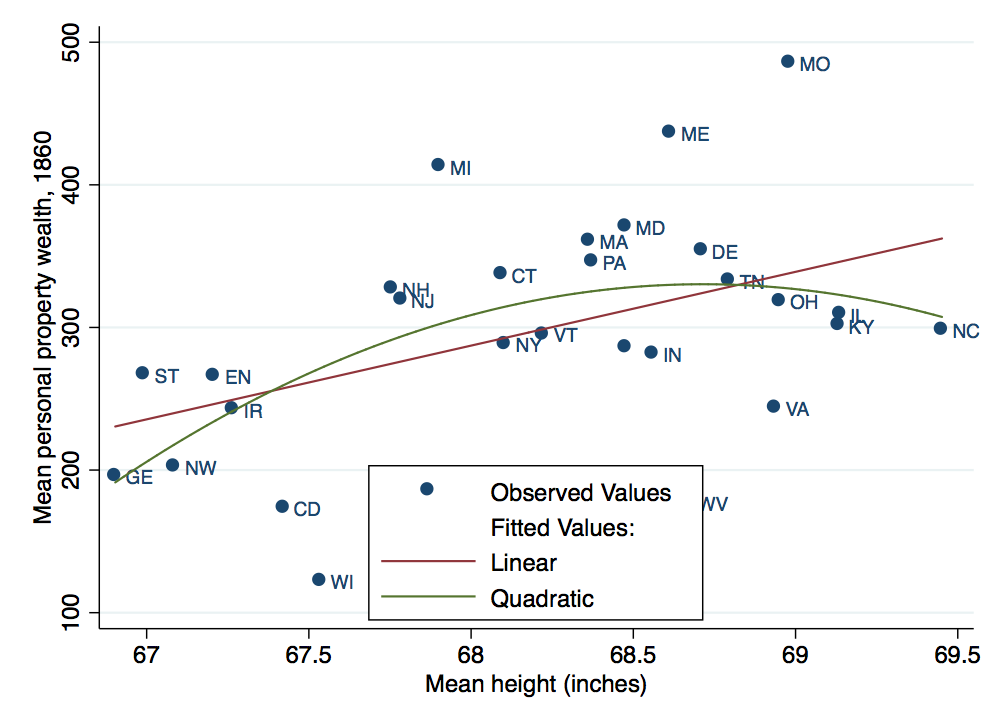
Here we have plotted a quadratic fit, using qfit, in addition to the linear fit. We have also added a legend to keep track of the different plots. Several options were specified for the legend. To explore these options, take a look at Stata’s legend manual page.
Graphs are an invaluable tool for getting a handle on relationships within a dataset but they do have their limitations. Let’s turn to doing some basic regression analysis to get a different sense of what the data are telling us. First things first, we need to clear out our collapsed data and go back to our recruit-level dataset.
. clear . use UA-complete-data-wide-format.dta
We will start with a basic linear regression exploring whether recruit wealth varies systematically with recruit height using the regress command:
. reg recprp1860 total_height white
Source │ SS df MS Number of obs = 4,235
─────────────┼────────────────────────────────── F(2, 4232) = 1.25
Model │ 596758.479 2 298379.239 Prob > F = 0.2879
Residual │ 1.0138e+09 4,232 239563.243 R-squared = 0.0006
─────────────┼────────────────────────────────── Adj R-squared = 0.0001
Total │ 1.0144e+09 4,234 239591.026 Root MSE = 489.45
─────────────┬────────────────────────────────────────────────────────────────
recprp1860 │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
total_height │ 4.153139 2.746063 1.51 0.131 -1.230586 9.536864
white │ 85.3717 185.1524 0.46 0.645 -277.6242 448.3676
_cons │ -67.81951 264.3912 -0.26 0.798 -586.1651 450.526
─────────────┴────────────────────────────────────────────────────────────────
The first variable we specify is the dependent variable (recprp_1860). This is followed by our independent variables (total_height and white). The regression output table provides a wealth of information. Likely of greatest interest are the coefficient estimates and their standard errors. Suppose that we wanted to see how well our regression is predicting personal wealth. We can do this using the predict command:
. predict wealth_residual, r (1,919 missing values generated)
By specifying the r option, Stata create a new variable wealth_residual equal to the difference between a recruit’s actual wealth and the wealth predicted using the coefficients in the regression results and the recruit’s own values for height and the white indicator variable. To see how well our prediction worked by state, let’s tabulate our birth states and summarize these residuals:
. tab rb_stat1, sum(wealth_residual)
│ Summary of Residuals
rb_stat1 │ Mean Std. Dev. Freq.
────────────┼────────────────────────────────────
AL │ 95.625977 400.97479 3
BE │ -108.76147 120.64942 3
BN │ -111.787 117.55146 3
BO │ 64.570335 356.49011 2
BV │ -125.49495 88.293154 8
CA │ -91.659386 0 1
CD │ -119.3492 182.7311 80
CT │ 30.913111 752.04254 43
DC │ -255.53994 34.543196 2
DE │ 50.669736 536.40594 71
EN │ -36.620345 332.67967 108
EU │ -137.50624 0 1
FR │ -28.612213 264.76746 15
GE │ -100.85835 198.32879 204
HA │ -63.005096 342.40716 4
HO │ -26.490013 235.91902 5
IA │ -168.27194 134.05315 4
IL │ 7.238567 384.91716 136
IN │ -16.589223 344.05276 352
IR │ -49.409029 512.02526 187
KY │ 1.7312117 385.2567 200
LA │ 163.42178 0 1
MA │ 70.754967 587.40162 70
MD │ 72.340744 746.85635 49
ME │ 136.79144 869.53231 55
MI │ 122.39604 877.39352 32
MK │ -262.46567 11.804247 2
MO │ 181.19645 1054.4056 36
MS │ -140.62109 0 1
MX │ -197.92967 26.487804 2
NB │ -206.19537 0 1
NC │ 11.41991 234.12099 27
NH │ 27.198542 430.03203 85
NJ │ 23.92747 501.35261 79
NM │ -200.3044 22.40206 5
NS │ -122.00977 91.7516 5
NW │ -86.800431 150.70824 19
NY │ -13.533896 388.82768 593
OH │ 22.568996 463.39087 609
PA │ 43.950211 699.81774 563
PR │ 18.996057 413.67502 5
PU │ -101.0897 143.90606 14
RI │ 33.85976 165.11677 4
SC │ 99.442915 317.66041 5
SN │ -195.81252 0 1
ST │ -16.026306 296.1281 25
SW │ -103.67332 178.82302 10
SZ │ 56.547218 433.00183 11
TN │ 35.342939 524.21783 77
US │ -178.87225 102.39513 2
VA │ -55.379443 284.27971 100
VT │ -5.1305059 333.32967 98
WI │ -168.30552 46.337342 10
WL │ -128.45367 50.036918 3
WR │ -225.33881 38.583983 3
WV │ -125.89062 153.23293 32
────────────┼────────────────────────────────────
Total │ -.35798986 484.23541 4,066
As we would expect, the overall mean for the residuals is quite close to zero. However, the means within each state vary substantially suggesting that we may want to control for birth state in our regression. We could create a series of indicator variables, one for each birth state and inclue those indicators as independent variables. However, we can instead take a shortcut by using Stata’s interactive expansion command. This command will automatically create all of the necessary indicator variables to cover the different values of a categorical variable and include them in your regression. Let’s give it a shot:
. xi: reg recprp1860 total_height white i.rb_stat1
i.rb_stat1 _Irb_stat1_1-62 (_Irb_stat1_1 for rb_stat1==AL omitted)
note: _Irb_stat1_2 omitted because of collinearity
note: _Irb_stat1_6 omitted because of collinearity
note: _Irb_stat1_16 omitted because of collinearity
note: _Irb_stat1_20 omitted because of collinearity
note: _Irb_stat1_27 omitted because of collinearity
note: _Irb_stat1_46 omitted because of collinearity
Source │ SS df MS Number of obs = 4,066
─────────────┼────────────────────────────────── F(57, 4008) = 0.98
Model │ 13082619.7 57 229519.644 Prob > F = 0.5231
Residual │ 940918148 4,008 234760.017 R-squared = 0.0137
─────────────┼────────────────────────────────── Adj R-squared = -0.0003
Total │ 954000767 4,065 234686.536 Root MSE = 484.52
──────────────┬────────────────────────────────────────────────────────────────
recprp1860 │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
──────────────┼────────────────────────────────────────────────────────────────
total_height │ 2.337147 2.925044 0.80 0.424 -3.397565 8.07186
white │ 74.21554 184.8014 0.40 0.688 -288.0981 436.5291
_Irb_stat1_2 │ 0 (omitted)
_Irb_stat1_3 │ -211.6514 395.7822 -0.53 0.593 -987.6046 564.3018
_Irb_stat1_4 │ -214.3743 395.7681 -0.54 0.588 -990.2998 561.5513
_Irb_stat1_5 │ -42.25426 442.6722 -0.10 0.924 -910.138 825.6295
_Irb_stat1_6 │ 0 (omitted)
_Irb_stat1_7 │ -227.0986 328.1631 -0.69 0.489 -870.4808 416.2837
_Irb_stat1_8 │ -195.76 559.6425 -0.35 0.727 -1292.97 901.4504
_Irb_stat1_9 │ -220.7542 285.0868 -0.77 0.439 -779.6828 338.1745
_Irb_stat1_10 │ -69.63469 289.4404 -0.24 0.810 -637.0987 497.8294
_Irb_stat1_11 │ -349.1986 442.3159 -0.79 0.430 -1216.384 517.9866
_Irb_stat1_12 │ -48.48164 285.6432 -0.17 0.865 -608.5012 511.5379
_Irb_stat1_13 │ -138.329 283.7658 -0.49 0.626 -694.6678 418.0097
_Irb_stat1_14 │ -243.4228 559.7214 -0.43 0.664 -1340.788 853.9424
_Irb_stat1_15 │ -130.1099 306.5835 -0.42 0.671 -731.1841 470.9643
_Irb_stat1_16 │ 0 (omitted)
_Irb_stat1_17 │ -203.6738 282.0252 -0.72 0.470 -756.6 349.2525
_Irb_stat1_18 │ -165.9707 370.2474 -0.45 0.654 -891.8614 559.92
_Irb_stat1_19 │ -130.2274 354.0848 -0.37 0.713 -824.4305 563.9757
_Irb_stat1_20 │ 0 (omitted)
_Irb_stat1_21 │ -265.1086 370.0637 -0.72 0.474 -990.6392 460.4221
_Irb_stat1_22 │ -90.94337 282.8365 -0.32 0.748 -645.4601 463.5734
_Irb_stat1_23 │ -115.5444 280.9782 -0.41 0.681 -666.418 435.3292
_Irb_stat1_24 │ -151.2785 282.1522 -0.54 0.592 -704.4537 401.8968
_Irb_stat1_25 │ -96.41638 281.8575 -0.34 0.732 -649.0138 456.181
_Irb_stat1_26 │ 70.21714 559.4896 0.13 0.900 -1026.693 1167.128
_Irb_stat1_27 │ 0 (omitted)
_Irb_stat1_28 │ -28.94185 285.7447 -0.10 0.919 -589.1604 531.2767
_Irb_stat1_29 │ -27.40518 288.2506 -0.10 0.924 -592.5366 537.7262
_Irb_stat1_30 │ 37.47845 287.3273 0.13 0.896 -525.8428 600.7997
_Irb_stat1_31 │ 21.71461 292.6703 0.07 0.941 -552.0819 595.5111
_Irb_stat1_32 │ -362.9343 442.3734 -0.82 0.412 -1230.232 504.3635
_Irb_stat1_33 │ 82.75822 291.1958 0.28 0.776 -488.1474 653.6638
_Irb_stat1_34 │ -245.1757 559.6608 -0.44 0.661 -1342.422 852.0706
_Irb_stat1_35 │ -304.7543 442.6722 -0.69 0.491 -1172.638 563.1295
_Irb_stat1_36 │ -303.94 559.4864 -0.54 0.587 -1400.844 792.9644
_Irb_stat1_37 │ -86.59375 294.8948 -0.29 0.769 -664.7515 491.564
_Irb_stat1_38 │ -73.4036 284.7446 -0.26 0.797 -631.6613 484.8541
_Irb_stat1_39 │ -76.54976 285.1071 -0.27 0.788 -635.5182 482.4186
_Irb_stat1_40 │ -301.4994 353.9574 -0.85 0.394 -995.4526 392.4538
_Irb_stat1_41 │ -217.212 353.8443 -0.61 0.539 -910.9436 476.5196
_Irb_stat1_42 │ -189.2284 301.2128 -0.63 0.530 -779.773 401.3162
_Irb_stat1_43 │ -113.9746 280.5513 -0.41 0.685 -664.0111 436.0619
_Irb_stat1_44 │ -76.0744 280.4679 -0.27 0.786 -625.9475 473.7987
_Irb_stat1_45 │ -55.76487 280.5591 -0.20 0.842 -605.8167 494.2869
_Irb_stat1_46 │ 0 (omitted)
_Irb_stat1_47 │ -81.01856 353.9143 -0.23 0.819 -774.8873 612.8502
_Irb_stat1_48 │ -202.6285 308.4033 -0.66 0.511 -807.2705 402.0136
_Irb_stat1_49 │ -70.46784 370.3239 -0.19 0.849 -796.5086 655.5729
_Irb_stat1_50 │ 1.244292 353.8679 0.00 0.997 -692.5336 695.0222
_Irb_stat1_51 │ -298.0971 559.5788 -0.53 0.594 -1395.183 798.9884
_Irb_stat1_52 │ -118.1475 296.2317 -0.40 0.690 -698.9262 462.6313
_Irb_stat1_53 │ -204.0511 319.0422 -0.64 0.522 -829.5512 421.449
_Irb_stat1_54 │ -46.7692 315.83 -0.15 0.882 -665.9716 572.4332
_Irb_stat1_55 │ -63.79064 285.197 -0.22 0.823 -622.9354 495.3542
_Irb_stat1_56 │ -286.3778 442.7183 -0.65 0.518 -1154.352 581.5962
_Irb_stat1_57 │ -154.2023 283.9497 -0.54 0.587 -710.9017 402.4971
_Irb_stat1_58 │ -104.6124 284.0553 -0.37 0.713 -661.5187 452.294
_Irb_stat1_59 │ -270.1621 319.5931 -0.85 0.398 -896.7424 356.4181
_Irb_stat1_60 │ -231.0409 395.7681 -0.58 0.559 -1006.967 544.8846
_Irb_stat1_61 │ -329.2881 395.8363 -0.83 0.406 -1105.347 446.7713
_Irb_stat1_62 │ -225.0256 292.6116 -0.77 0.442 -798.707 348.6558
_cons │ 167.2927 394.1977 0.42 0.671 -605.5539 940.1394
──────────────┴────────────────────────────────────────────────────────────────
Notice that after including indicator variables for birth state, the coefficients on both height and white are substantially reduced. The previous coefficients were picking up average differences across states in height and wealth. Including the state indicator variables is effectively controlling for average differences across states and is instead exploiting within state variation in height and wealth.