25 September 2019
For the first part of this exercise, we will be using the Stata data file us-wid-data.dta. This file is based on the data available through the World Wealth and Income Database. To generate the data set, I used the following commands in Stata:
For the second part of this exercise, we will use data from the Integrated Public Use Microdata Series. IPUMS provides an incredibly convenient interface for downloading samples of historical federal census data as well as a wide range of other datasets. There are two different datasets that I constructed through IPUMS: 1870-census-wealth-data.dta and 1940-census-income-data.dta. Both of these are available on the course website. You can create your own census extracts using the IPUMS website after creating a free account.
Now let’s go ahead and get started by opening the WID data file. When we open it, we will first clear out Stata’s memory just in case a file is already open:
. clear . use us-wid-data.dta
If you are working on your own computer, the WID package is the easiest way to get the wealth and income data in Stata. If you are on a campus computer, Stata will not let you install the package. Instead, you can download a copy of the us-wid-data.dta file from our course website. If you would like additional variables or data from other countries, you can also use the data download tools on the WID website to generate your own samples.
Before we can work with the data, it will be useful to reshape the data. Let’s list the data for a single year to look at the current structure of the dataset:
. list if year == 1980
┌──────────────────────────────────────────────────┐
│ country variable percen~e year value │
├──────────────────────────────────────────────────┤
17. │ US shweal992j p0p1 1980 -.00423 │
68. │ US shweal992j p0p10 1980 -.01058 │
121. │ US shweal992j p0p50 1980 .01055 │
172. │ US shweal992j p50p100 1980 .98939 │
223. │ US shweal992j p75p100 1980 .87975 │
├──────────────────────────────────────────────────┤
325. │ US shweal992j p90p100 1980 .65102 │
427. │ US shweal992j p95p100 1980 .49045 │
529. │ US shweal992j p99p100 1980 .23554 │
580. │ US sptinc992j p0p1 1980 -.00033 │
631. │ US sptinc992j p0p10 1980 .0102 │
├──────────────────────────────────────────────────┤
684. │ US sptinc992j p0p50 1980 .19894 │
735. │ US sptinc992j p50p100 1980 .8011 │
786. │ US sptinc992j p75p100 1980 .56004 │
888. │ US sptinc992j p90p100 1980 .34243 │
990. │ US sptinc992j p95p100 1980 .23904 │
├──────────────────────────────────────────────────┤
1092. │ US sptinc992j p99p100 1980 .10671 │
└──────────────────────────────────────────────────┘
Notice that each year has multiple observations, one for each of our key income or wealth variables. This is what Stata refers to as data in long format. We would prefer to have one observation per year with all of the income and wealth variables included, this will let us easily compare values over time (for example, graphing how both the bottom decile and top decile shares of income evolve over time). This is called data in wide format. Stata’s reshape command converts between long and wide format. Before we use it, let’s restrict our data to just one of the outcomes (wealth share or income share) to make it a bit simpler to see what is going on:
. keep if variable == "shweal992j"
(563 observations deleted)
. rename value wealth
. reshape wide wealth, i(year) j(percentile) string
(note: j = p0p1 p0p10 p0p50 p50p100 p75p100 p90p100 p95p100 p99p100)
Data long -> wide
─────────────────────────────────────────────────────────────────────────────
Number of obs. 563 -> 102
Number of variables 5 -> 11
j variable (8 values) percentile -> (dropped)
xij variables:
wealth -> wealthp0p1 wealthp0p10 ... wealthp99p100
─────────────────────────────────────────────────────────────────────────────
Now we can see what the new format of the data looks like:
. list if year == 1980
┌─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┐
│ year wealth~1 wealt~10 wealt~50 w~50p100 w~75p100 w~90p100 w~95p100 we~9p100 country variable │
├─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┤
68. │ 1980 -.00423 -.01058 .01055 .98939 .87975 .65102 .49045 .23554 US shweal992j │
└─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┘
Notice that all of the wealth percentiles for a given year are now included in a single observation. Also notice that Stata has created new variable names for us, combining the name of our key variable for reshaping, wealth, with the value of our j variable, percentile in this case. This makes it much easier to compare two different parts of the distribution over time. For example, let’s just list the shares for bottom and top halves of the distribution for the 1990s:
. list year wealthp0p50 wealthp50p100 if year>1989 & year<2000
┌─────────────────────────────┐
│ year wealt~50 we~50p100 │
├─────────────────────────────┤
78. │ 1990 .02192 .97807 │
79. │ 1991 .0215 .97845999 │
80. │ 1992 .019 .98107 │
81. │ 1993 .01764 .98234 │
82. │ 1994 .01575 .98428 │
├─────────────────────────────┤
83. │ 1995 .01367 .98633 │
84. │ 1996 .01241 .98759 │
85. │ 1997 .00997 .99005001 │
86. │ 1998 .00959 .99036 │
87. │ 1999 .01052 .98951 │
└─────────────────────────────┘
Much easier than having a separate observation for each outcome in each year.
One downside of keeping only the wealth variable is that we may want to look at wealth and income inequality trends side by side. We can do this by creating a second dataset with income data and then merging the two datasets back together. First, we’ll save our wealth data and then follow the same steps we took above to create an income inequality dataset.
. save us-wealth-data.dta, replace
file us-wealth-data.dta saved
. clear
. use us-wid-data.dta
. keep if variable == "sptinc992j"
(563 observations deleted)
. rename value income
. reshape wide income, i(year) j(percentile) string
(note: j = p0p1 p0p10 p0p50 p50p100 p75p100 p90p100 p95p100 p99p100)
Data long -> wide
─────────────────────────────────────────────────────────────────────────────
Number of obs. 563 -> 102
Number of variables 5 -> 11
j variable (8 values) percentile -> (dropped)
xij variables:
income -> incomep0p1 incomep0p10 ... incomep99p100
─────────────────────────────────────────────────────────────────────────────
. save us-income-data.dta, replace
file us-income-data.dta saved
To merge the data, we will use Stata’s merge command. When using this command, we need a variable to merge on. In this case, we want to merge on year, combining the wealth and income data from each file into a single observation per year in a new file. First, we need to sort our data on this merge variable:
. clear . use us-wealth-data.dta . sort year . save us-wealth-data.dta, replace file us-wealth-data.dta saved . clear . use us-income-data.dta . sort year . save us-income-data.dta, replace file us-income-data.dta saved
Now we can issue the merge command. Note that there should be one observation per year in each of the datasets. Therefore, we are doing what is called a one to one merge and using the 1:1 option for the merge command. If we had one dataset with a single observation per year and another dataset with multiple observations per year, we would need to do a one to many merge, using the 1:m option. Let’s merge our data:
. merge 1:1 year using us-wealth-data.dta
Result # of obs.
─────────────────────────────────────────
not matched 0
matched 102 (_merge==3)
─────────────────────────────────────────
Notice that we specified the type of merge, the variable we are merging on and the file name we are merging the current dataset with. Stata has created a new variable named _merge that keeps track of merging successes and failures. A value of three indicates an observation that was successfully merged between the two datasets. A value of one indicates an observation from the master dataset (the one originally open) that could not be merged to the using dataset. A value of two indicates an observation from the using dataset that could note be merged to the master dataset.
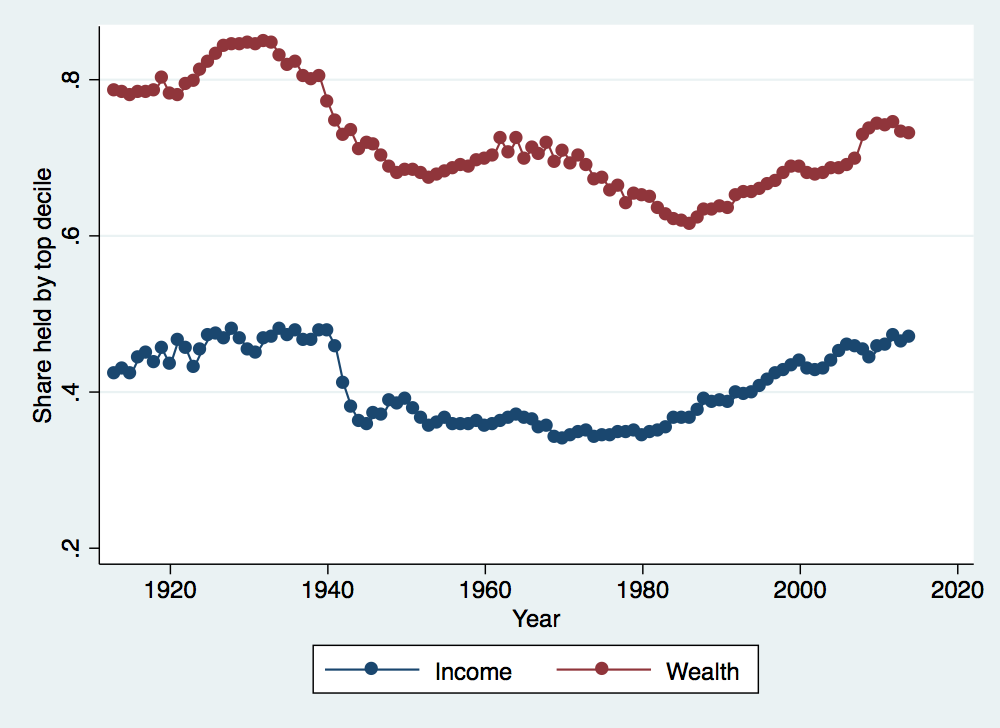
Let’s start by looking at trends in the share of income and wealth held over time by the top decile. To do this, a good approach is to create a twoway graph in Stata. Note that there are many, many options for graphs in Stata and tweaking these options can be very complicated but leads to much better graphs. The easiest approach is to create your first graph from the Graphics menu, selecting all of the various options from the various graphical menus. Once you create the graph, Stata will actually issue the command that includes all of your options. You can copy this command and paste it into a do file so that you can automatically create the same graph or slightly modify the command to tweak the graph appearance without going back through all of the menus.
. twoway (connected incomep90p100 year if year>1900 & year<2020) (connected wealthp90p100 year if year>1900 & year<2020, sort) > , ytitle(Share held by top decile) xtitle(Year) legend(order(1 "Income" 2 "Wealth")) . graph export income_and_wealth_over_time.png, width(500) replace (file income_and_wealth_over_time.png written in PNG format)

Now let’s construct a ratio of the share of income held by the top decile relative to the share held by the bottom decile and graph its evolution over time.
. gen income_ratio = incomep90p100 / incomep0p10 (51 missing values generated) . twoway (connected income_ratio year if year>1959 & year<2018), ytitle(Ratio) xtitle(Year) legend(off) . graph export income_ratio_over_time.png, width(500) replace (file income_ratio_over_time.png written in PNG format)
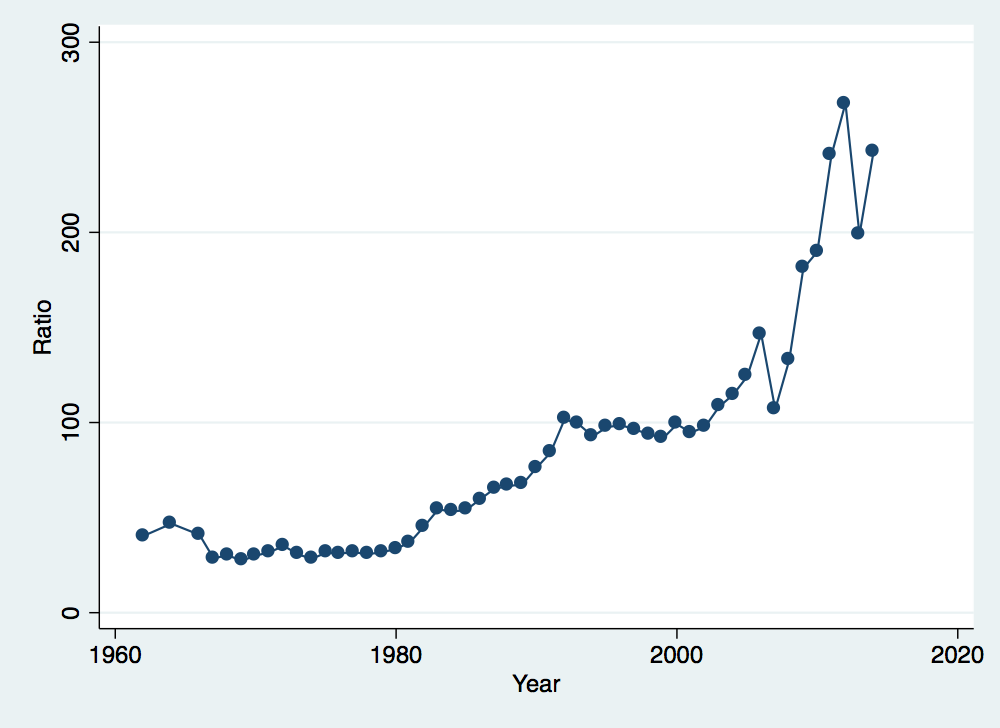
What if we worry that this pattern is being driven by the incomes of the top one percent? Let’s get rid of those and see how the pattern changes:
. replace income_ratio = (incomep90p100 - incomep99p100) / incomep0p10 (51 real changes made) . twoway (connected income_ratio year if year>1959 & year<2018), ytitle(Ratio) xtitle(Year) legend(off) . graph export income_ratio_over_time_no_top.png, width(500) replace (file income_ratio_over_time_no_top.png written in PNG format)
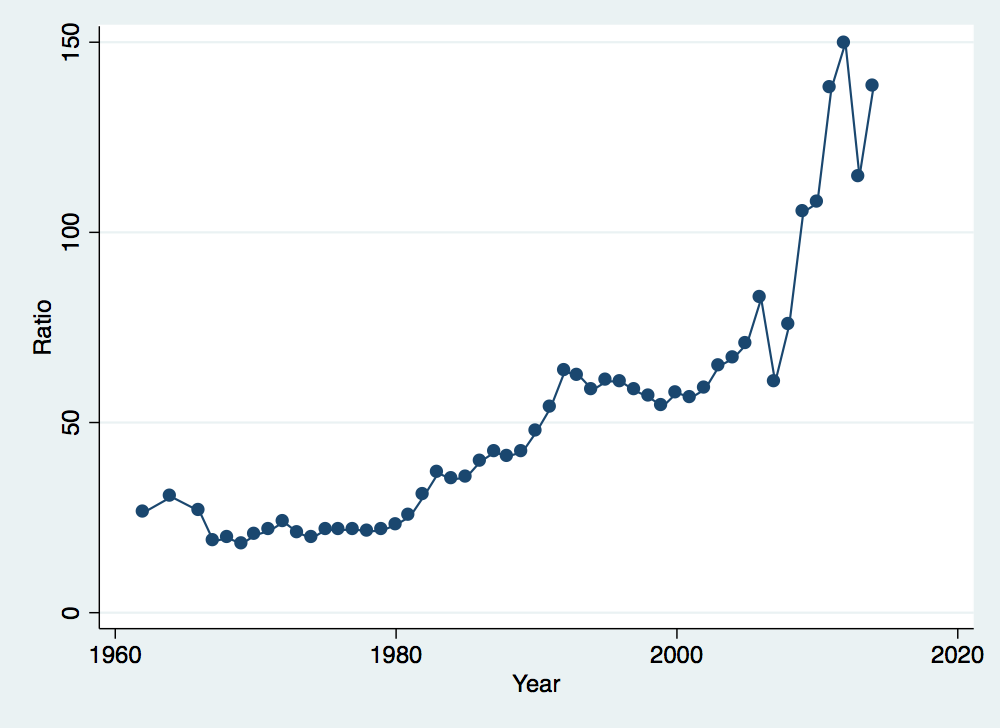
Something very strange has happened. The scale has shifted (the ratios on the vertical axis are now much smaller) but the patterns over time are identical to the previous graph. Is this possible? Think about what we discussed in class about top coding incomes and how that might affect this particular graph.
Take some time to generate your own samples from the WID data to look at more dimensions of wealth and income inequality over time and across countries.
Now let’s switch our attention to the individual-level data available through the federal census. We will start with our 1870 federal census data. The 1870 census is nice for our purposes because it asked individuals to report wealth in terms of both real property and personal property, offering a chance to look at historical wealth distributions as a function of individual demographic characteristics. Let’s load the data:
. clear . use 1870-census-wealth-data.dta
Our key wealth variables here are realprop and persprop. We also have a proxy for income in the form of occscore, the occupational income score. To see the variable descriptions, we can use the describe command:
. describe realprop persprop occscore
storage display value
variable name type format label variable label
──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
realprop long %12.0g Real estate value
persprop long %12.0g Value of personal estate
occscore byte %8.0g Occupational income score
. sum realprop persprop occscore
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
realprop │ 826,735 430.3513 4329.183 0 750000
persprop │ 826,735 203.9352 3158.798 0 800000
occscore │ 826,735 5.907386 10.12816 0 80
What we would like is a more detailed version of these summary statistics than what we get above. In particular, we would like to know what different percentiles of the distribution are, not just the value for the mean. Adding the detail option to summarize will do that for us:
. sum realprop if age>24 & age<60, detail
Real estate value
─────────────────────────────────────────────────────────────
Percentiles Smallest
1% 0 0
5% 0 0
10% 0 0 Obs 292,573
25% 0 0 Sum of Wgt. 292,573
50% 0 Mean 934.4765
Largest Std. Dev. 5938.434
75% 0 700000
90% 2000 700000 Variance 3.53e+07
95% 4800 750000 Skewness 47.01049
99% 15000 750000 Kurtosis 4164.42
. sum persprop if age>24 & age<60, detail
Value of personal estate
─────────────────────────────────────────────────────────────
Percentiles Smallest
1% 0 0
5% 0 0
10% 0 0 Obs 292,573
25% 0 0 Sum of Wgt. 292,573
50% 0 Mean 447.5396
Largest Std. Dev. 4355.338
75% 200 580000
90% 800 580000 Variance 1.90e+07
95% 1500 800000 Skewness 79.0654
99% 6000 800000 Kurtosis 10870.25
That is helpful, but it doesn’t really tell us the share of wealth held by various groups. That is going to require a bit of calculation on our part. Let’s calculate the share of wealth held by the top 10%, top 5% and top 1%. Starting with the top 10%, notice from our detailed summary output that the 90th percentile for personal property is 800 and that the total amount of personal property is 130938016 (the mean times the number of observations). Now if we summarize personal property for just the top 10%, we can get our share:
. local all_persprop = r(sum)
. sum persprop if age>24 & age<60 & persprop>800, detail
Value of personal estate
─────────────────────────────────────────────────────────────
Percentiles Smallest
1% 850 803
5% 915 803
10% 1000 805 Obs 27,781
25% 1000 805 Sum of Wgt. 27,781
50% 1580 Mean 3953.659
Largest Std. Dev. 13634.74
75% 3000 580000
90% 6870 580000 Variance 1.86e+08
95% 11000 800000 Skewness 26.35241
99% 40000 800000 Kurtosis 1164.433
. local top10_persprop = r(sum)
. local top10_share = `top10_persprop'/`all_persprop'
Our share held by the top 10% is simply the sum of wealth given above divided by our original sum. This gives us a share of .8388443.
Notice the use of local in the Stata code above. This is taking advantage of what Stata calls local macros. Local macros can be used to store a value that you would like to use later. In this case, I wanted to store the sum of wealth for the full distribution so that I could use it later to calculate the share of wealth. r(sum) is a returned result from the previous command. For any command, you can look at the help page to see what results are returned.
Now let’s look at inequality in wealth ownership across different groups. We will start with regions. We can take a quick look at differences in wealth across regions by tabulating region and then summarizing one of our wealth variables:
. tab region if age>24 & age<60, sum(realprop)
Census │
region and │ Summary of Real estate value
division │ Mean Std. Dev. Freq.
────────────┼────────────────────────────────────
New Engla │ 872.63409 4427.1482 28,160
Middle At │ 1224.7045 7422.0723 67,465
East Nort │ 1272.275 5324.6876 64,629
West Nort │ 1029.9564 4487.6752 27,485
South Atl │ 432.28811 3065.3537 46,367
East Sout │ 495.61992 2988.5577 33,127
West Sout │ 424.09165 7150.2515 16,323
Mountain │ 317.69527 2091.3255 2,645
Pacific D │ 1796.1817 17913.125 6,372
────────────┼────────────────────────────────────
Total │ 934.47654 5938.4343 292,573
. tab region if age>24 & age<60, sum(persprop)
Census │
region and │ Summary of Value of personal estate
division │ Mean Std. Dev. Freq.
────────────┼────────────────────────────────────
New Engla │ 629.65323 4914.8569 28,160
Middle At │ 606.90019 6765.8082 67,465
East Nort │ 478.78251 3855.3038 64,629
West Nort │ 447.76766 2154.3861 27,485
South Atl │ 203.66004 1746.0229 46,367
East Sout │ 260.07743 1455.3993 33,127
West Sout │ 225.62709 2414.5558 16,323
Mountain │ 318.15577 1486.8318 2,645
Pacific D │ 1008.978 7632.8686 6,372
────────────┼────────────────────────────────────
Total │ 447.53964 4355.3381 292,573
Mean real property wealth is highest in the Midwest (the East North Central and West North Central regios) and far, far lower in the South (the South Atlantic, East South Central and West South Central regions). These patterns largely hold for personal property as well, except that New Englanders jump to the top in terms of average wealth. If you think of the occupational and land distributions of these regions, these patterns in personal and real property wealth should make some sense.
Now let’s focus on the share of wealth held by the top 5% by in the Northeast, the Midwest and the South. To do this, we will need to condition on region number. Our tabulation above shows the variable labels, not their actual values. A quick way to see the values is to simultaneously tabulate and summarize the variable:
. tab region, sum(region)
Census │ Summary of Census region and
region and │ division
division │ Mean Std. Dev. Freq.
────────────┼────────────────────────────────────
New Engla │ 11 0 68,997
Middle At │ 12 0 174,995
East Nort │ 21 0 184,716
West Nort │ 22 0 79,068
South Atl │ 31 0 143,943
East Sout │ 32 0 106,210
West Sout │ 33 0 49,472
Mountain │ 41 0 6,018
Pacific D │ 42 0 13,316
────────────┼────────────────────────────────────
Total │ 22.712209 8.6164153 826,735
Now we can see that the Northeast includes regions 11 and 12, the Midwest includes regions 21 and 22, and the South includes regions 31, 32 and 33. With this information, we can now calculate some wealth shares:
. sum realprop if age>24 & age<60 & (region==11 | region==12), detail
Real estate value
─────────────────────────────────────────────────────────────
Percentiles Smallest
1% 0 0
5% 0 0
10% 0 0 Obs 95,625
25% 0 0 Sum of Wgt. 95,625
50% 0 Mean 1121.026
Largest Std. Dev. 6682.971
75% 0 300000
90% 2500 300000 Variance 4.47e+07
95% 5500 700000 Skewness 39.37928
99% 18000 700000 Kurtosis 3008.161
. local northeast_real_total = r(sum)
. local northeast_p95 = r(p95)
. sum realprop if age>24 & age<60 & (region==11 | region==12) & realprop>`northeast_p95', detail
Real estate value
─────────────────────────────────────────────────────────────
Percentiles Smallest
1% 5800 5530
5% 6000 5530
10% 6000 5540 Obs 4,740
25% 7000 5540 Sum of Wgt. 4,740
50% 10000 Mean 15984.7
Largest Std. Dev. 25517.34
75% 15000 300000
90% 26200 300000 Variance 6.51e+08
95% 40000 700000 Skewness 12.32997
99% 110000 700000 Kurtosis 254.7475
. local northeast_p95_sum = r(sum)
. local northeast_p95_share = `northeast_p95_sum'/`northeast_real_total'
So for the Northeast, the top 5% share of total real property wealth is 0.707. Let’s do the same for personal property:
. sum persprop if age>24 & age<60 & (region==11 | region==12), detail
Value of personal estate
─────────────────────────────────────────────────────────────
Percentiles Smallest
1% 0 0
5% 0 0
10% 0 0 Obs 95,625
25% 0 0 Sum of Wgt. 95,625
50% 0 Mean 613.6006
Largest Std. Dev. 6277.668
75% 200 580000
90% 1000 580000 Variance 3.94e+07
95% 2000 800000 Skewness 69.82736
99% 10000 800000 Kurtosis 7330.01
. local northeast_pers_real_total = r(sum)
. local northeast_pers_p95 = r(p95)
. sum persprop if age>24 & age<60 & (region==11 | region==12) & persprop>`northeast_pers_p95', detail
Value of personal estate
─────────────────────────────────────────────────────────────
Percentiles Smallest
1% 2120 2015
5% 2400 2015
10% 2500 2028 Obs 4,302
25% 3000 2028 Sum of Wgt. 4,302
50% 5000 Mean 10179.29
Largest Std. Dev. 27879.3
75% 9000 580000
90% 20000 580000 Variance 7.77e+08
95% 30000 800000 Skewness 16.65667
99% 90000 800000 Kurtosis 395.4652
. local northeast_pers_p95_sum = r(sum)
. local northeast_pers_p95_share = `northeast_pers_p95_sum'/`northeast_pers_real_total'
This gives us a top 5% share of total personal property of 0.746. Repeat this exercise for the other regions and see if the concentration of personal and real property by region matches your priors.
Finally, we will look at inequality in wealth across race. To do this, let’s try a new technique of collapsing the data by region and race. This command basically averages individual level data across groups, producing a much smaller and more manageable group-level dataset. We want to compare levels of wealth across races within regions, so we want our group level to be race by region (we’ll have one observation for Southern whites, one observation for Southern blacks, one observation for Midwestern whites, and so on). First we need to construct a better region variable and drop any irrelevant observations:
. gen better_region = "Northeast" if region==11 | region==12 (582,743 missing values generated) . replace better_region = "Midwest" if region==21 | region==22 (263,784 real changes made) . replace better_region = "South" if region==31 | region==32 | region==33 (299,625 real changes made) . drop if better_region=="" | age<25 | age>59 (543,179 observations deleted)
Now we are ready to collapse our data. We are going to collapse by race and our new region variable. We have to decide what sort of average values we want to generate. Let’s keep mean wealth and median wealth:
. collapse (mean) persprop_mean = persprop realprop_mean = realprop (p50) persprop_median = persprop realprop_median = realpro
> p, by(race better_region)
. list
┌────────────────────────────────────────────────────────────────────────────────────────────────┐
│ race better_~n perspro~ean realpro~ean pers~ian real~ian │
├────────────────────────────────────────────────────────────────────────────────────────────────┤
1. │ White Midwest 482.116471 1230.239057 0 0 │
2. │ White Northeast 627.0172547 1143.842886 0 0 │
3. │ White South 379.7344112 776.8343765 0 0 │
4. │ Black/African American/Negro Midwest 72.30855693 245.4412618 0 0 │
5. │ Black/African American/Negro Northeast 73.51948052 202.7597403 0 0 │
├────────────────────────────────────────────────────────────────────────────────────────────────┤
6. │ Black/African American/Negro South 22.68433376 19.5449889 0 0 │
7. │ American Indian or Alaska Native Midwest 75.20833333 230.8333333 0 0 │
8. │ American Indian or Alaska Native Northeast 0 0 0 0 │
9. │ American Indian or Alaska Native South 131.5789474 720 0 0 │
10. │ Chinese Northeast 0 0 0 0 │
└────────────────────────────────────────────────────────────────────────────────────────────────┘
Notice that we now have one observation per race per region. It turns out that our median wealth is not all that interesting: median wealth for both personal and real property is zero across all groups in all regions. However, the mean wealth data demonstrates the enormous wealth gap between white and black individuals in 1870. You can try collapsing by points in the wealth distribution or collapsing over different geographic areas to explore the data further.
Now we will turn to our final dataset, the income and education data available in the 1940 federal census. This is the first federal census with income and years of education and the last census with publicly available microdata (each federal census becomes public after a 72-year waiting period). Let’s open up the 1940 census data and see what we’re working with:
. clear
. use 1940-census-income-data.dta
. describe
Contains data from 1940-census-income-data.dta
obs: 1,351,732
vars: 23 12 Feb 2018 08:07
size: 71,641,796
──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
storage display value
variable name type format label variable label
──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
year int %8.0g year_lbl Census year
datanum byte %8.0g Data set number
serial double %8.0f Household serial number
hhwt double %10.2f Household weight
region byte %43.0g region_lbl
Census region and division
stateicp byte %41.0g stateicp_lbl
State (ICPSR code)
statefip byte %57.0g statefip_lbl
State (FIPS code)
county int %8.0g County
urban byte %8.0g urban_lbl
Urban/rural status
pernum int %8.0g Person number in sample unit
perwt double %10.2f Person weight
relate byte %24.0g relate_lbl
Relationship to household head [general version]
sex byte %8.0g sex_lbl Sex
age int %36.0g age_lbl Age
race byte %32.0g race_lbl Race [general version]
nativity byte %46.0g nativity_lbl
Foreign birthplace or parentage
higrade byte %24.0g higrade_lbl
Highest grade of schooling [general version]
higraded int %38.0g higraded_lbl
Highest grade of schooling [detailed version]
educ byte %25.0g educ_lbl Educational attainment [general version]
educd int %46.0g educd_lbl
Educational attainment [detailed version]
incwage long %12.0g Wage and salary income
incnonwg byte %39.0g incnonwg_lbl
Had non-wage/salary income over $50
occscore byte %8.0g Occupational income score
──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Sorted by:
The key variable for our purposes is really incwage which captures pre-tax wage and salary income. We could go ahead and start looking at the distribution of incwage but there is a big problem: IPUMS uses 999998 as the code for not in the universe and 999999 as the code for missing. If we leave these in the data, we will mistakenly transform missing observations into very rich individuals. Let’s create a new income variable that gets rid of these values and then take a look at its distribution by both sex and race:
. gen income = incwage if incwage~=999998 & incwage~=999999 (336,811 missing values generated) . gen ln_income = ln(income) (932,456 missing values generated)
. histogram ln_income if age>24 & age<60, percent ytitle(Percent) xtitle(Log Income) by(sex) . graph export inc-distribution-by-sex.png, width(500) replace (file inc-distribution-by-sex.png written in PNG format)
. histogram ln_income if age>24 & age<60 & (race==1 | race==2), percent ytitle(Percent) xtitle(Log Income) by(race) . graph export inc-distribution-by-race.png, width(500) replace (file inc-distribution-by-race.png written in PNG format)
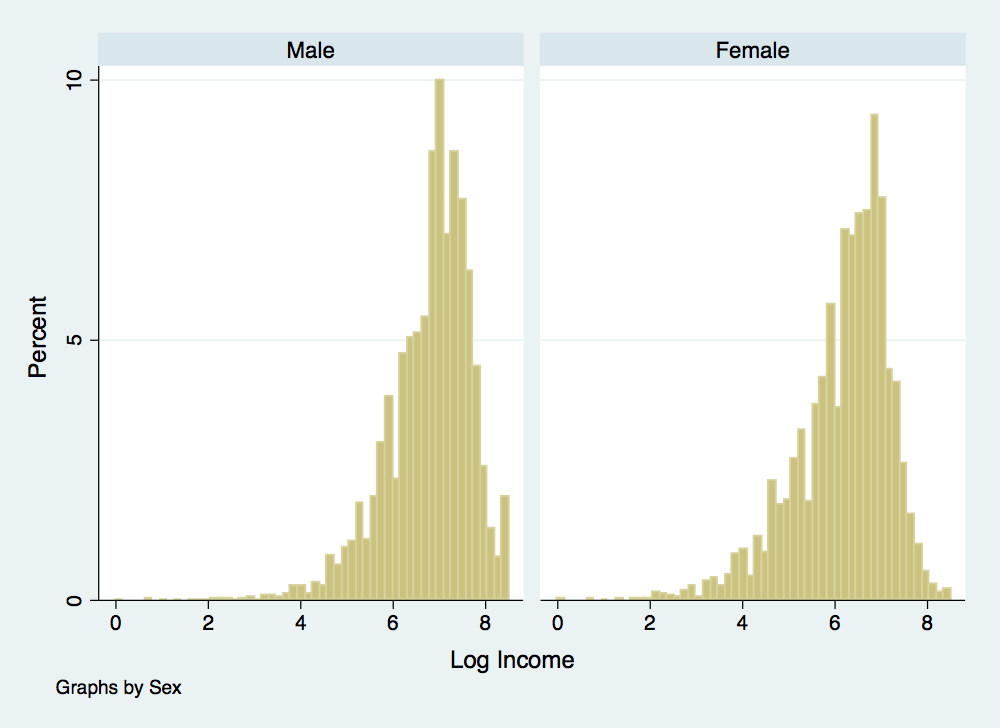
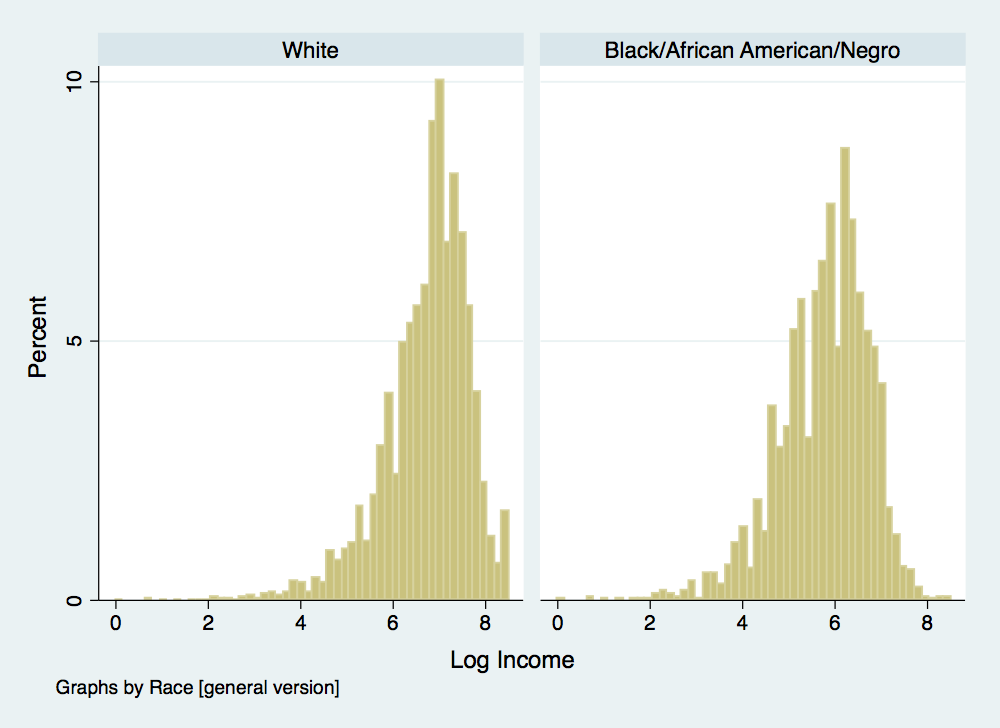
There is something a little deceptive about these income distributions. Recall one of our problems with using log income when estimating mobility rates: individuals reporting zero income are dropped since you cannot take the log of zero. To understand why this is a bit problematic, we will summarize income and log income by race and generate a variable to designate individual’s reporting an income of zero:
. gen zero_income = 0 if income>0 & income~=.
(932,456 missing values generated)
. replace zero_income = 1 if income==0
(595,645 real changes made)
. * Note that race==1 for white and race==2 for black
. sum income ln_income zero_income if age>24 & age<60 & race==1
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
income │ 550,492 569.5389 863.4532 0 5001
ln_income │ 264,937 6.745254 .932867 0 8.517393
zero_income │ 550,492 .5187269 .4996496 0 1
. sum income ln_income zero_income if age>24 & age<60 & race==2
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
income │ 55,962 254.9826 387.8304 0 5001
ln_income │ 29,878 5.783654 .9809142 0 8.517393
zero_income │ 55,962 .466102 .4988541 0 1
Notice that the fraction of white adults with an income of zero is larger than the fraction of black adults with an income of zero. This might seem odd at first, suggesting that employment outcomes were better for black adults than for white adults. However, there are two other things that may be going on here. Let’s dig a little deeper into the data.
. gen zero_income_overall = zero_income
(336,811 missing values generated)
. replace zero_income_overall = 0 if incnonwg == 2
(167,864 real changes made)
. sum income ln_income zero_income zero_income_overall if age>24 & age<60 & race==1
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
income │ 550,492 569.5389 863.4532 0 5001
ln_income │ 264,937 6.745254 .932867 0 8.517393
zero_income │ 550,492 .5187269 .4996496 0 1
zero_incom~l │ 550,492 .3621506 .4806225 0 1
. sum income ln_income zero_income zero_income_overall if age>24 & age<60 & race==2
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
income │ 55,962 254.9826 387.8304 0 5001
ln_income │ 29,878 5.783654 .9809142 0 8.517393
zero_income │ 55,962 .466102 .4988541 0 1
zero_incom~l │ 55,962 .306458 .4610263 0 1
What we have done above is account for non-wage income in addition to wage and salary income. This has reduced the fraction of both black and white individuals with no income, but has not eliminated the black-white gap. Let’s look at one last thing:
. * Note that sex==1 for male and sex==2 for female
. sum income ln_income zero_income zero_income_overall if age>24 & age<60 & race==1 & sex==1
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
income │ 276,068 950.8008 997.8441 0 5001
ln_income │ 201,118 6.872841 .8839883 0 8.517393
zero_income │ 276,068 .2714911 .4447296 0 1
zero_incom~l │ 276,068 .0639516 .2446672 0 1
. sum income ln_income zero_income zero_income_overall if age>24 & age<60 & race==2 & sex==1
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
income │ 26,760 406.3284 456.4466 0 5001
ln_income │ 18,996 6.040882 .8731689 0 8.517393
zero_income │ 26,760 .2901345 .4538328 0 1
zero_incom~l │ 26,760 .082997 .2758829 0 1
Now we are looking just at adult males. Notice that our employment gap has reversed, white males are less likely to have zero income than black males, and our income gap has become more pronounced. The different labor force participation patterns of white and black females have substantial impacts on what the summary statistics look like and any inferences based on those statistics.
Now let’s take advantage of the educational attainment data and think about wage gaps by education level. First, let’s see how the educational attainment data is coded:
. tab educ, sum(educ)
Educational │
attainment │ Summary of Educational attainment
[general │ [general version]
version] │ Mean Std. Dev. Freq.
────────────┼────────────────────────────────────
N/A or no │ 0 0 183,660
Nursery s │ 1 0 202,223
Grade 5, │ 2 0 500,947
Grade 9 │ 3 0 77,531
Grade 10 │ 4 0 80,394
Grade 11 │ 5 0 50,453
Grade 12 │ 6 0 161,625
1 year of │ 7 0 20,790
2 years o │ 8 0 24,484
3 years o │ 9 0 10,416
4 years o │ 10 0 28,581
5+ years │ 11 0 10,628
────────────┼────────────────────────────────────
Total │ 2.8246465 2.4416302 1,351,732
We will start by generating indicator variables for several educational categories: eight years or less, some high school, high school grad, some college, college grad.
. gen common_school = 0 if educ~=. . replace common_school = 1 if educ<3 (886,830 real changes made) . gen some_hs = 0 if educ~=. . replace some_hs = 1 if educ>2 & educ<6 (208,378 real changes made) . gen hs_grad = 0 if educ~=. . replace hs_grad = 1 if educ==6 (161,625 real changes made) . gen some_col = 0 if educ~=. . replace some_col = 1 if educ>6 & educ<10 (55,690 real changes made) . gen col_grad = 0 if educ~=. . replace col_grad = 1 if educ>9 (39,209 real changes made)
Now we can run a really simple regression capturing the relationship between education and log earnings, giving us an estimate of the returns to education:
. reg ln_income common_school some_hs some_col col_grad if age>24 & age<60
Source │ SS df MS Number of obs = 295,886
─────────────┼────────────────────────────────── F(4, 295881) = 6550.75
Model │ 23214.2056 4 5803.5514 Prob > F = 0.0000
Residual │ 262131.912 295,881 .885936954 R-squared = 0.0814
─────────────┼────────────────────────────────── Adj R-squared = 0.0813
Total │ 285346.118 295,885 .964381829 Root MSE = .94124
──────────────┬────────────────────────────────────────────────────────────────
ln_income │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
──────────────┼────────────────────────────────────────────────────────────────
common_school │ -.4758037 .0048874 -97.35 0.000 -.4853829 -.4662245
some_hs │ -.1698294 .0059714 -28.44 0.000 -.1815331 -.1581257
some_col │ .1265731 .0080291 15.76 0.000 .1108363 .1423098
col_grad │ .4394552 .0080426 54.64 0.000 .4236919 .4552186
_cons │ 6.892993 .0042761 1611.97 0.000 6.884612 6.901374
──────────────┴────────────────────────────────────────────────────────────────
Notice that I included all of the indicator variables for education levels except for high school grad. In general, when you are including indicator variables to capture different values for a categorical variable, you must omit one indicator. If you do not, you will run into a big problem of multicollinearity and the coefficients cannot be uniquely identified. In practice, Stata will drop one of the variables in this case so that the regression can be run but it is nicer to choose for yourself which category to omit. The coefficients on the included indicator variables then measure the difference in the outcome relative to to the omitted category. So in this case, the coefficient on col_grad is measuring the additional earning for a college grad relative to a high school grad.
Now let’s do a slightly better job of estimating the returns to education by including controls we know influence earnings. We will construct variables for experience, age squared, and experience squared and generate indicators for race and sex:
. gen experience = age - (higrade + 2) . replace experience = age - 5 if higrade == 1 (183,660 real changes made) . gen age_2 = age^2 . gen experience_2 = experience^2 . gen female = 0 if sex==1 (674,165 missing values generated) . replace female = 1 if sex==2 (674,165 real changes made) . gen black = 0 if race==1 (143,180 missing values generated) . replace black = 1 if race==2 (137,114 real changes made)
Now we can run a better version of the above regression:
. reg ln_income common_school some_hs some_col col_grad age age_2 experience experience_2 black female if age>24 & age<60
Source │ SS df MS Number of obs = 294,815
─────────────┼────────────────────────────────── F(10, 294804) = 10277.19
Model │ 73447.3598 10 7344.73598 Prob > F = 0.0000
Residual │ 210685.755 294,804 .714663829 R-squared = 0.2585
─────────────┼────────────────────────────────── Adj R-squared = 0.2585
Total │ 284133.115 294,814 .963770768 Root MSE = .84538
──────────────┬────────────────────────────────────────────────────────────────
ln_income │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
──────────────┼────────────────────────────────────────────────────────────────
common_school │ -.0835449 .0073238 -11.41 0.000 -.0978994 -.0691905
some_hs │ -.048543 .0059165 -8.20 0.000 -.0601391 -.0369469
some_col │ -.0521658 .007554 -6.91 0.000 -.0669715 -.0373601
col_grad │ .0161879 .0088892 1.82 0.069 -.0012348 .0336105
age │ .1919434 .0030665 62.59 0.000 .1859332 .1979536
age_2 │ -.0011768 .0000322 -36.57 0.000 -.0012398 -.0011137
experience │ -.0895515 .0018664 -47.98 0.000 -.0932097 -.0858934
experience_2 │ .0000886 .0000233 3.80 0.000 .000043 .0001343
black │ -.5867135 .0055239 -106.21 0.000 -.5975401 -.5758869
female │ -.629986 .0036412 -173.02 0.000 -.6371227 -.6228493
_cons │ 3.509519 .047373 74.08 0.000 3.416669 3.602368
──────────────┴────────────────────────────────────────────────────────────────
This now gives us a better estimate of the returns to education and gives us estimates of gender and racial gaps in earnings after controlling for education, age and experience levels. However, there is still a pretty big problem. Average incomes and average education levels differ substantially across regions (check this for yourself with the data). This is going to potentially bias many of our coefficients. We should probably be controlling for region. We can do this in the same way we did for our education categories, generating a series of indicator variables and including all of them (except for one) in the regression. However, we can also take a shortcut by using Stata’s interactive expansion command. This command will create indicator variables for any categorical variable:
. xi: reg ln_income common_school some_hs some_col col_grad age age_2 experience experience_2 black female i.region if age>24
> & age<60
i.region _Iregion_11-42 (naturally coded; _Iregion_11 omitted)
Source │ SS df MS Number of obs = 294,815
─────────────┼────────────────────────────────── F(18, 294796) = 6596.68
Model │ 81584.2695 18 4532.45942 Prob > F = 0.0000
Residual │ 202548.846 294,796 .68708139 R-squared = 0.2871
─────────────┼────────────────────────────────── Adj R-squared = 0.2871
Total │ 284133.115 294,814 .963770768 Root MSE = .8289
──────────────┬────────────────────────────────────────────────────────────────
ln_income │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
──────────────┼────────────────────────────────────────────────────────────────
common_school │ -.1471102 .0072418 -20.31 0.000 -.161304 -.1329163
some_hs │ -.0786446 .0058154 -13.52 0.000 -.0900426 -.0672466
some_col │ .0007922 .0074359 0.11 0.915 -.013782 .0153664
col_grad │ .0793048 .0087917 9.02 0.000 .0620734 .0965362
age │ .1665501 .0030321 54.93 0.000 .1606072 .172493
age_2 │ -.0010157 .0000316 -32.10 0.000 -.0010778 -.0009537
experience │ -.0706882 .0018541 -38.12 0.000 -.0743222 -.0670541
experience_2 │ -.0000502 .0000229 -2.19 0.029 -.0000951 -5.18e-06
black │ -.4934027 .0056127 -87.91 0.000 -.5044034 -.482402
female │ -.6369779 .0035749 -178.18 0.000 -.6439847 -.6299711
_Iregion_12 │ .0927184 .0063393 14.63 0.000 .0802935 .1051432
_Iregion_21 │ -.0044005 .0064506 -0.68 0.495 -.0170434 .0082425
_Iregion_22 │ -.3026446 .0076456 -39.58 0.000 -.3176298 -.2876595
_Iregion_31 │ -.1532237 .0071458 -21.44 0.000 -.1672292 -.1392181
_Iregion_32 │ -.4111879 .0084058 -48.92 0.000 -.427663 -.3947127
_Iregion_33 │ -.3893858 .0078546 -49.57 0.000 -.4047805 -.3739911
_Iregion_41 │ -.2731964 .0108344 -25.22 0.000 -.2944315 -.2519614
_Iregion_42 │ -.0740597 .0076829 -9.64 0.000 -.089118 -.0590014
_cons │ 3.988974 .0471479 84.61 0.000 3.896565 4.081382
──────────────┴────────────────────────────────────────────────────────────────
Now we get college education premiums that look a bit more reasonable.